fMRI: Biological Basis and Experiment Design Lecture 22: GLM 101 - PowerPoint PPT Presentation
Title:
fMRI: Biological Basis and Experiment Design Lecture 22: GLM 101
Description:
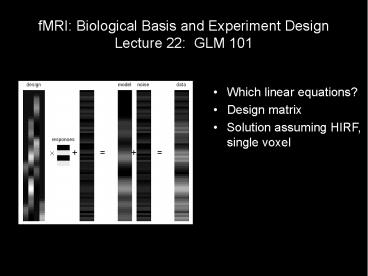
fMRI: Biological Basis and Experiment Design Lecture 22: GLM 101 Which linear equations? Design matrix Solution assuming HIRF, single voxel + = = + Linear algebra ... – PowerPoint PPT presentation
Number of Views:63
Avg rating:3.0/5.0
Title: fMRI: Biological Basis and Experiment Design Lecture 22: GLM 101
1
fMRI Biological Basis and Experiment
DesignLecture 22 GLM 101
- Which linear equations?
- Design matrix
- Solution assuming HIRF, single voxel
?
2
Linear algebra
A1x1 A2x2 A3x3 A4x4 y
is the same as
Ax y
where
x1 x2 x3 x4
A
x
A1 A2 A3 A4
3
Linear algebra
A1,1x1 A2,1x2 A3,1x3 A4,1x4 y1 A1,2x1
A2,2x2 A3,2x3 A4,2x4 y2 A1,3x1 A2,3x2
A3,3x3 A4,3x4 y3 A1,mx1 A2,mx2 A3,mx3
A4,mx4 ym
y1 y2 y3 ym
x1 x2 x3 x4
A1,1 A2,1 A3,1 A4,1 A1,2 A2,2 A3,2
A4,2 A1,3 A2,3 A3,3 A4,3 A1,m A2,m A3,m
A4,m
A
x
y
4
Linear model for BOLD in a voxel
Ax y
Design matrix, m x n - m time-points - n
stimulus types
Data m x 1 - response through time
Responses n x 1 - for each stimulus, a scalar
(single number) representing how well that voxel
responds to that stimulus
y1 y2 y3 ym
x1 x2 x3 x4
A1,1 A2,1 A3,1 A4,1 A1,2 A2,2 A3,2
A4,2 A1,3 A2,3 A3,3 A4,3 A1,m A2,m A3,m
A4,m
A
x
y
5
Design matrix
stim 1
stim 2
stim 3
stim 1
stim 2
stim 3
Matrix form for GLM
6
Design matrix assuming shape of HIRF
stim 1
stim 2
stim 3
stim 1
stim 2
stim 3
time
?
7
Design matrix modeling data
A
stim 1
stim 2
stim 3
BOLD
x
?
8
Solving linear model for BOLD in a voxel
measured
known
Ax y
... the answer
9
Solving linear model for BOLD in a voxel
Ax y ATAx ATy (ATA)-1(ATA)x (ATA)-1ATy x
(ATA)-1ATy
10
Solving linear model for BOLD in a voxel
x (ATA)-1ATy
y
(ATA)-1AT
1 0 0.5
x
11
Linear model for BOLD in a voxel, with noise
A(x ?) y ? where A design matrix
nTimepoints x nStimTypes , x concatenated
responses nStimTypes x 1, y true response
nTimepoints x 1 ? noise in data
nTimepoints x 1 ? error in estimating
response nStimTypes x 1 Solution xest x
? (ATA)-1AT (y ?), so ? (ATA)-1AT ?
12
A(x ?) y ? xest x ?
(ATA)-1AT (y ?)
0.96 -0.18 0.49
y ?
xest
1 0 0.5
x
Axest
13
Example block design with linear trend
Design matrix
Solution
x 1 0.2 xest 1.01 0.24
14
Example block design with linear trend
Design matrix
Solution
x -0.5 0.2 xest -0.46 0.25






![CS3104: ?????? Principles of Digital Design [project2] floating-point number addition PowerPoint PPT Presentation](https://s3.amazonaws.com/images.powershow.com/8016500.th0.jpg?_=20160728018)























