HYDROLOGIC STATISTICS PowerPoint PPT Presentation
Title: HYDROLOGIC STATISTICS
1
HYDROLOGIC STATISTICS
- Summary Statistics (Moments Product and
L-moments) - Distributional(Magnitude andFrequency) Analysis
- NonparametricStatistics (Intro-duction to
Hypo-thesis Testing) - Trend Testing
- Rank Sum Test
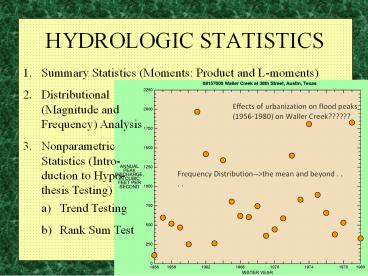
Effects of urbanization on flood peaks
(1956-1980) on Waller Creek??????
Frequency Distribution--gtthe mean and beyond . .
. .
2
PROBABILITY DISTRIBUTIONS
- Discrete and Continuous Random Variables
- Cumulative Distribution Function (cdf)
- expressed as functions
- have parameters
- Quantile Functions
- Statistical Expectation
- Quantiles
- median, quartiles, interquartile range
- plotting position estimators
- Plotting Positions1. order data x1 x2 ...
xn2. rankem 1, 2, ..., n (i is rank)3. F(x)
i-0.40/n0.2 Cunnane plotting-positions F(x)
i/n1 Weibull plotting-positions
3
MORE PLOTTING POSITION STUFF
- PLOTTING POSITIONS
- 1. order data x1 x2 ... xn2. rankem 1, 2,
..., n (i is rank) - 3. F(x) nonexceedance probability or just the
percentile. - 4. 1-F(x) exceedance probability
- GENERAL FORMULA
- 1-F(x) (i-a) / (n1-2a)
- Cunnane plotting-positions (a0.40)
- F(x) (i-0.40)/(n0.2)approx. quantile
unbiased - Weibull plotting-positions (a0)
- F(x) i/(n1)unbiased F(x) for all
distributions - Hazen plotting-positions (a0.50)
- F(x) (i-0.5)/nlong legacy
- Blom plotting-positions (a0.375)
- F(x) (i-3/8)/(n1/4) optimal for normal
distribution
The true probability associated with the largest
(and smallest) observation is a random variable
with mean 1/(n1) and a standard deviation of
nearly 1/(n1). Hence, all plotting position
formula give crude estimates of the unknown
probabilities associated with largest and
smallest events.
http//pubs.usgs.gov/twri/twri4a3/
See chapter 2
4
Comal Springs Daily Mean Flow
5
Comal Springs Daily Mean Flow
6
(Flow) Duration Curves--I
- Simple, yet highly informative graphical
summaries of the variability of a (daily) time
series--Streamflow (flow-duration) - An FDC is a graph plotting the magnitude of a
variable Q verses fraction of time the Q does not
exceed a specified value Q(F). The fraction of
time can be thought of as probability and
cumulative fraction of time is termed
nonexceedance probability (F). - The probability refers to the frequency or
probability of nonexceedance (or exceedance) in a
suitably long period of time rather than
probability of exceedance on a specific time
interval (daily).
7
(Flow) Duration Curves--II
- Area under the curve is equal to the average for
the period. - Other statistics or statistical concepts visible
include median, quartiles, other percentiles,
variability, and skewness. Steeper curves are
associated with increasingly variable data. - The slopes and changes in the slope of the curves
can be important diagnostics of streamflow
conditions in a watershed.
8
(Flow) Duration Curves--III
- Duration curves for neighboring stations yield
valuable insights into hydrologic or
hydrogeologic processes
9
(Flow) Duration Curves--IV
- For natural streams
- Slope of FDC for upper end is determined by
regional climate and characteristics of large
precipitation events. - Slope of the lower end is determined by geology,
soils, topography. - Slope of the upper end is relatively flat where
snowmelt is the principal cause of floods and for
large streams where floods are caused by long
duration storms. Flashy watersheds and
watersheds effected by short duration storms have
steep upper ends. - A flat lower end slope usually indicates that
flows come from significant storage in ground
water aquifers or frequency precipitation inputs.
10
SUMMARY STATISTICS
- Product Moments (PMs)
- L-momentsseen already, butwill study in
detaillater in the semester.
See powers--product
Theoretical PMs----gt
E Expectation operator
In terms of PDF
In terms of quantile function
11
SUMMARY STATISTICS
Sample PMs----gt
Biased Estimators
12
SUMMARY STATISTICS
- Summary Statistics
The uniformly minimum unbiased estimator of the
standard deviation.
PM Boundness!!!Careful in hydrologic data sets.
13
NONPARAMETRIC STATISTICS
Nonparametric statistics (NP) are a branch of
statistics based on the ranking or ranks of the
data rather than the data values themselves.
This fact has many desirable properties in
hydrologic data analysis because data sets are
often highly variable, measured with large error,
censored, contaminated, and a host of other
problems.
- NP require fewer assumptions about the
distribution generating the data. The normal or
bell-shape curve assumption is NOT required. - NP are easier than classical statistics to apply.
- NP are remarkably(?) straightforward to
understand.
14
NONPARAMETRIC STATISTICS
- NP can be used in situations that normal theory
or classical statistics can not. - NP seem to sacrifice too much information. This
is NOT the case. More often than not, NP are
only slightly less efficient than classical
statistics when distributions are normal. NP can
be absurbly more efficient than classical
statistics. - NP are robust in the presence of outliers,
contaminated data, censored data, highly skewed
data and so on. - Hollander, M., and Wolfe, D.A., 1973,
Nonparametric statistical methods John Wiley
Inc., New York, 503 p.
15
NP STATISTICSTrend Testing
Trend Testingthat is the testing for temporal
(time) trendsin data might be the most common
use of NP in physical hydrology. Therefore,
well use trend testing as a starting point for
introduction.
Trend Testing Relation Testing Independence
TestingKENDALLS TAU
16
Kendalls TauNP Trend Testing
- We have n bivariate observations (X1,Y1), . . . ,
(Xn,Yn). - We want to test whether there is a relation
between the Xs and the Ys. We can not test for
cause and effectsvery important to remember. - We assume that each data pair are mutually
independent and each pair is derived from the
same population.
17
Kendalls TauNP Trend Testing
- Define Kendalls Tau by t 2Prob(X1-X2)(Y1-Y2)
gt 0 - 1t 0 if Xs and Ys are unrelated
because half of the time the X differences and Y
differences would have the same sign. t
2 (1/2) - 1 0 -1 t 1 - For each 1 i lt j ncalculate x(Xi,Xj,Yi,Yj)
x(a,b,c,d) score for . . . 1 if (a-b)(c-d) gt
0 0 if (a-b)(c-d) 0-1 if (a-b)(c-d) lt 0
18
Kendalls TauNP Trend Testing
- Sum up ones and minus ones and calculate the sum
(K) K S(i1,n-1)S(ji1,n)x(a,b,c,d)There
are n(n-1)/2 terms to compute. - Compute t 2K/n(n-1), which is known as
Kendalls Rank Correlation Coefficient or simply
Kendalls Taut estimates the probability
parameter Prob(X1-X2)(Y1-Y2) gt 0 (t1)/2t
will generally be lower than values of the
traditional correlation coefficient for linear
associations of equal strength. Strong linear
correlations of r gt 0.9 correspond to t gt 0.7. t
measures all monotonic correlations (linear or
nonlinear), and does not change with monotonic
power transformations of X and/or Y for example,
log(X).
19
Kendalls TauNP Trend Testing
- Hypothesis TestingWe know that inherent
randomness will produce a range of t differing
from zero. If we know the distribution of t,
hence K under conditions in which t 0, we can
perform a test by specifying some error or some
tolerance in being right or wrong about whether
the data is independent. - Start with hypothesis, the Null Hypothesis, Ho,
that the data is independent at the a level of
significance, thena a1 a2 often it is
taken that a1 a2 - reject Ho(t 0) if K k(a2,n) or K -k(a1,n)
- accept Ha(t ? 0) if K lt k(a2,n) or K gt -k(a1,n)
- k is the null distribution of K, which we will
investigate in more detail. - We can also test whether t gt 0, which means
positive correlation between X and Y or whether t
lt 0 (negative correlation.)
20
Kendalls TauNP Trend Testing
t gt 0 at the a significant level reject Ho(t
0) if K k(a,n) accept Ha(t gt 0) if K lt
k(a,n) t lt 0 at the a significant level reject
Ho(t 0) if K -k(a,n) accept Ha(t lt 0) if K gt
-k(a,n)
21
CIRCULAR STATISTICS
- Circular statistics are used to quantify the time
of occurrence of hydrologic variables on a
circletypically on a yearly basis. - Successive samples of circular statistic
results - The math (
- Really comprehensive analysis
22
Circular Statisticssee BOX 4-3
- Circular statistics are used to quantify the time
of occurrence of hydrologic variables on a
circletypically on a yearly basis. - Two values require calculation
- Average Time of Occurrence (Angle of the Mean) -
analogous to the arithmetic mean - Index of Seasonality - analogous to the standard
deviation
The average hydrologic quantity (say a monthly
value) is considered to be a vector quantity.
Length is proportional to the amount and
direction (angle) of the time of the value.
23
Circular Statistics
- Average Time of Occurrence (Angle of the Mean)
- Time through the year (or other interval) is
represented on a circle with (usually) each month
assigned an angle. - Think of the sin/cos terms as weight factors.
- Resultant Angle Prime fR atan(S/C)
- Resultant Angle (deal with quadrant)fR fR
if(S gt 0 and C gt 0)fR fR180 if(C lt 0)fR
fR360 if(S lt 0 and C gt 0)
But other conversions are sometimes needed
depending upon the output of the atan function.
24
Circular Statistics
- Resultant Angle (deal with quadrant)PHI (
(Sterm gt 0 and Cterm gt 0)
or - (Sterm gt 0 and Cterm lt 0) )
? PHIp PHIp360 fR
fR fR fR360 if(S gt 0 and C gt 0)
or (S lt 0 and C lt 0) - 2. Index of Seasonality (IS) PR sqrt(S2
C2) IS PR / (Total of Xm Values)
In the Perl language
25
Circular Statistics
List of examples of hydrologic variables on
which circular statistics would be useful
Example Total Rainfall 36 inches-------------
------------------------------------Season
Rainfall sin cos-----------------------------
--------------------Spring (Mar.31DoY90)
4.00 0.9998 0.0215Summer(Jun.30DoY181) 16
.00 .0258 -.9997Fall (Sept.30DoY273) 11.
00 -.9999 -.0129Winter(Dec.31DoY365)
5.00 .0000 1.0000-------------------------
------------------------S -6.587 C -11.05
fatan(S/C)gt 30.8 degreesf 30.8 180 211
degreesPR 12.87 IS 12.87/36 0.357
26
Circular Statistics for 08155500 Barton Springs
at Austin, Texas
- 1978 to 2003
- Vector lengths are short
- No definitive angle
- Are these observations consistent with your
expectation?
27
Circular Statistics for 08158000 Colorado River
at Austin, Texas
- 1899 to 2003
- Vector lengths are moderately long.
- Concentration of angle near end of September to
(through?) November. - Are these observations consistent with your
expectation?
28
Circular Statistics for 08169000 Comal River at
NewBraunfels, Texas
- 1933 to 2002
- Vector lengths are short
- No definitive angle--but perhaps more in January
through March?
29
Circular Statistics for 08169000 Comal River at
NewBraunfels, Texas
30
Circular Statistics for 08169000 Comal River at
NewBraunfels, Texas
31
ExtensiveCircularStatistics