Aim: What is an Euler Path and Circuit? PowerPoint PPT Presentation
1 / 14
Title: Aim: What is an Euler Path and Circuit?
1
Aim What is an Euler Path and Circuit?
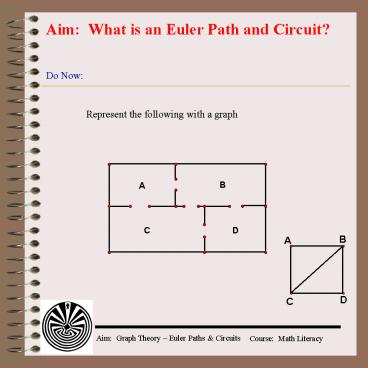
Do Now
Represent the following with a graph
2
Euler Path
Euler Path a path that travels through every
edge of a graph once and only once. Each edge
must be traveled and no edge can be retraced.
A,
B,
E,
D,
B,
C,
E,
D,
G
F,
3
Euler Path
Euler Circuit a circuit that travels through
every edge of a graph once and only once, and
must begin and end at the same vertex.
A,
B,
E,
D,
F,
B,
C,
E,
D,
G,
A
Every Euler circuit is an Euler path
Not every Euler path is an Euler circuit
Some graphs have no Euler paths
Other graphs have several Euler paths
Some graphs with Euler paths have no Euler
circuits
4
Euler Theorem
- Eulers Theorem
- The following statements are true for connected
graphs - If a graph has exactly two odd vertices, then it
has at least one Euler path, but no Euler
circuit. Each Euler path must start at one of
the odd vertices and end at the other. - If a graph has no odd vertices (all even
vertices), it has at least one Euler circuit. An
Euler circuit can start and end at any vertex. - If a graph has more than two odd vertices, then
it has no Euler paths and no Euler circuits.
5
Model Problem
Explain why the graph has at least one Euler path.
number of edges at each vertex
degree 2
degree 4
degree 4
2
A
D
3
B
E
3
4
C
4
Two odd vertices
degree 3
degree 3
- If a graph has exactly two odd vertices, then it
has at least one Euler path, but no Euler
circuit. Each Euler path must start at one of
the odd vertices and end at the other.
6
Model Problem
Find a Euler path.
5
6
2
3
4
7
1
8
D,
C,
B,
C,
A,
B,
D,
E
E,
7
Model Problem
Explain why the graph has a least one Euler
circuit.
degree 4
degree 4
degree 2
degree 2
degree 4
degree 4
no odd vertices
2. If a graph has no odd vertices (all even
vertices), it has at least one Euler circuit. An
Euler circuit can start and end at any vertex.
8
Model Problem
Find an Euler circuit.
11
10
12
9
13
3
8
4
2
14
1
7
5
6
H,
G,
E,
G,
I,
J,
H,
D,
C,
C,
A,
B,
D,
F,
H
Euler Circuit a circuit that travels through
every edge of a graph once and only once, and
must begin and end at the same vertex.
9
Graph Theorys Beginnings
In the early 18th century, the Pregel River in a
city called Konigsberg, surround an island before
splitting into two. Seven bridges crossed the
river and connected four different land area.
Many citizens wished to take a stroll that would
lead them across each bridge and return them to
the starting point without traversing the same
bridge twice. Possible?
They couldnt do it.
Euler proved that it was not possible.
10
The Theorem at Work
3. If a graph has more than two odd vertices,
then it has no Euler paths and not Euler circuits.
11
Model Problem
A, B, C, and D represent rooms. The outside of
the house is labeled E. The openings represent
doors. a) Is it possible to find a path that
uses each door exactly once?
degree 6
look for a Euler path or circuit
exactly 2 odd vertices
- If a graph has exactly two odd vertices, then it
has at least one Euler path, but no Euler
circuit. Each Euler path must start at one of
the odd vertices and end at the other.
12
Model Problem
A, B, C, and D represent rooms. The outside of
the house is labeled E. The openings represent
doors. b) If possible, find such a path.
10
9
7
2
1
3
8
6
4
5
start at one of the odd vertices
B,
E,
A,
D,
C,
A,
E,
C,
B,
E,
D
13
Fluerys Algorithm
- If Eulers Theorem indicates the existence of an
Euler path or Euler circuit, one can be found
using the following procedure. - If the graph has exactly two odd vertices, chose
one of the two odd vertices as the starting
point. If the graph has no odd vertices, choose
any vertex as the starting point. - Number edges as you trace through the graph
according to the following rules - After you traveled over an edge, change it
to a dashed line. - When faced with a choice of edges to trace,
choose an edge that is not a bridge (an edge,
which, if removed from a connected graph would
leave behind a disconnected graph). Travel over
an edge that is a bridge only if there is no
alternative.
14
Model Problem
The graph has at least one Euler circuit. Find
it using Fleurys Algorithm.
E
F
D
C
A
B
no odd vertices, begin at any vertex.