Lecture on Multi Access Communication

1
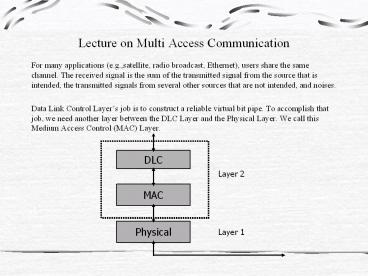
Lecture on Multi Access Communication

• For many applications (e.g.,satellite, radio
  broadcast, Ethernet), users share the same
  channel. The received signal is the sum of the
  transmitted signal from the source that is
  intended, the transmitted signals from several
  other sources that are not intended, and noises.
• Data Link Control Layers job is to construct a
  reliable virtual bit pipe. To accomplish that
  job, we need another layer between the DLC Layer
  and the Physical Layer. We call this Medium
  Access Control (MAC) Layer.

DLC
Layer 2
MAC
Physical
Layer 1
2
Queuing Problem in Multiple Access

• Each node has a queue of packets to be
  transmitted and channel is a common and shared
  resource (i.e., server).
• In the above model,
• Information is distributed.
• The server does not know which nodes contain
  packets.
• Nodes are unaware of packets at other nodes.

Node 1
Node i1
Channel
Node 2
Node i2
. . .
. . .
Node i
Node m
3
Extreme Solutions

• We may consider the following two extreme
  solutions. The actual solution will be somewhere
  in between.
• Free for all multiple access.
• Nodes send packets whenever they need
  to, hoping for no interference or collision.
• An important question is how and when to
  retransmit when collisions occur.
• Scheduled (dynamically or not) multiple access.
• A certain schedule is given for packet
  transmission in order to avoid a collision. An
  important question here is how to fix the
  scheduling. We must also consider how to transmit
  to the nodes the information about the schedule.

4
Example of Multiple Access Media
Satellite

• 1. Satellite Channel
• Separate antennas are needed for different
  geographical areas. We may consider for one area,
  TDM can be used while FDM can be used for others.
  However, this is very inefficient use of the
  expensive channel. We can reduce the delay and
  increase utilization by sharing the medium on a
  per demand basis. We, however, need a mechanism
  of mediating the potential collisions.

Area 1
Area k
Area 1

Ground Stations
5

• 2. Multi drop telephone lines.
• This is also known as party lines.
• 3.Multi tapped bus.
• Each node can receive signals sent by other
  nodes. Simultaneous transmissions causes a
  collision.

Primary
Secondaries
6

• 4. Packet radio network
• Each node is in the reception range of some sub
  network of nodes. For example, the nodes marked
  with can transmit simultaneously. A mechanism
  to mediate collisions is complex.

7
Example of Multiple Access System Slotted Aloha
Network

• Basic Assumptions
• Each packet requires one time unit or slot for
  transmission.
• There are m nodes each generating packets
  according to a Poisson process with rate ?/m.
• Over the defined medium, there are only two
  possibilities collision or perfect reception.
• There is a mechanism for immediate feedback.
  Immediately after any time slot, every node
  learns the results of the previous time slot
  (0,1,e) where 0 implies no packet was
  transmitted, 1 implies one packet was
  transmitted, and e implies there was a collision.
• Each packet involved in a collision will be
  retransmitted later until it is received
  correctly.
• 6. A node with packets for retransmission is said
  to be back logged. One of the following two is
  true
• If a packet is waiting for transmission or
  collided with another packet(s), all new arrivals
  are lost.
• There exists an infinite set of nodes and new
  arrivals arrive a new node each time.

slot
t
8
Slotted Aloha

• Each node sends its packet in the first slot
  after the packet arrival.
• Slotted Aloha will potentially reduce the delay.
• Slotted Aloha has a significant of collision
  risk.
• TDM has on the average m/2 slots of delay.
• When a collision occurs, the nodes involved will
  know at the end of slot, and become backlogged.
• Those collided nodes cannot re-send packets
  immediately since it creates a certain
  collision.
• It is required to wait for a random number of
  slots and retransmit.

9
Analysis

• Assume the infinite node case, i.e., 6b.
• Consider the total number of packets transmitted
  in the next time slot.
• The combine new arrival is Poisson with rate ?.
• There are also retransmissions from backlogged
  nodes.
• Assume that the total number of packets to be
  transmitted in the next time slot to be Poisson
  with rate G (gt?).
• The transmission is successful only if there is
  exactly one packet transmitted in a time
• slot, and therefore,
• because the transmission in the next time slot is
  Poisson with rate G, i.e.,

10

• At equilibrium,
• Arrival rate departure rate
• Maximum
  throughout 1/e ? 0.368
• Problem with this approach is that G is a
  function of the number of backlogged nodes, which
  is not reflected in this model.

11
More Precise Model

• Assume the no buffering case of 6a.
• Define
• qr probability that a backlogged node
  retransmit in a time slot
• X number of slots from collision until a
  backlogged node retransmits
• n number of backlogged nodes
• m total number of nodes generating packets
• m-n nodes are not backlogged, and they will
  transmit any fresh arrival takes place before the
  beginning of the next time slot.

12

• Let the probability that an unbacklogged node has
  a packet be qa.
• Since n is the number of backlogged nodes of the
  system (i.e., the state), from one to next time
  slot, n is increased by the number of new
  arrivals and is decreased by at most one if one
  packet is transmitted successfully.

13

• We can solve the above equations for pn where pn
  is the steady state probability of being in state
  n.

0
1
2
3
14

• We want to determine whether or not the system is
  stable.
• (The term stability will be defined later.)
• We want qr to be large to avoid unnecessary
  delays.
• If nqr gtgt1, then collision will occur in every
  slot and the system remains heavily
• backlogged.
• Determining qr involves tradeoffs.
• Define
• Dn expected changes in the number of backlogged
  node in one slot
• Psucc expected number of successful
  transmissions in one slot
• Then, since
  (m-n)qa is the expected number of new arrivals in
  one time slot. Therefore, Dn can be viewed as
  the expected drift of the state from n in one
  time slot.

15

• Let G(n) be the packet transmission attempt rate,
  i.e., at state n, the sum of new arrival rate and
  the retransmission rate from the backlogged
  nodes.
• G(n) expected number of attempted
  transmissions in a time slot
• when the system is
  in state n.
• (m-n)qa nqr ()
• Using () and () together, Psucc G(n)e-G(n).
• In the above, we used the fact that
  for small x.
• Then, Probability of idle slot .

16

• One desired stable state, one unstable state, and
  one undesired stable state.
• Maximum Psucc maximum departure rate 1/e

17

• If we use assumption 6b instead,
• One desired stable state, and one unstable state.

18
Stability Problem with Slotted Aloha

• If qr is increased, retransmission delay is
  reduced.
• Attempt rate G(n)(m-n)qa nqr increases with n
  faster for a larger qr .
• G(n) scale is contracted.
• Fewer packets are required to exceed unstable
  equilibrium.
• If qr is decreased, retransmission delay
  increases.
• ?G(n) scale is expanded.
• Only one stable point remains.
• Backlog is a large fraction of m.
• Large delay
• Many packets may be discarded.

19
Definitions

• Definition
• A multi access system is stable for a given
  arrival rate if the average delay per packet is
  finite.
• Definition
• Maximum throughput is the least upper bound of
  arrival rates for which system is stable.
• Slotted Aloha is unstable for any rate greater
  than zero,. Therefore, the maximum throughput of
  Slotted Aloha is zero.

20
Stabilizing Slotted Aloha Pseudo-Bayesian
Algorithm

• New arrivals are considered backlogged upon
  arrival. If there are n backlogged packets, the
  attempt rate is .
• Probability of successful transmission
• Algorithm keeps as estimate of backlog n in
  the beginning of each slot.
• Backlogged packets are then transmitted with
  probability
• This makes Gnqr to be near 1.
• Updating
• estimated backlog in beginning of kth slot.

21
Note

• Adding ? to previous backlog is due to new
  arrivals.
• max is to ensure the estimate is never less
  than the number of new arrivals.
• For successful transmission 1 is subtracted from
  previous backlog due to successful departure.
• Subtract 1 for idle to avoid too many idle
  slots.
• Add (e-2)-1 on collision to avoid too many
  collisions.
• For large , if n, each of n backlogged
  nodes retransmits with probability
• By Poisson approximation

22
Delay Analysis

• Define Wi be the delay from the arrival of ith
  packet until the beginning of ith successful
  transmission. In FIFO, Wi is the queuing delay of
  ith arrival.
• Average of Wi over all i is the average delay.
• Ri residual time to the beginning of next slot.
• ni number of backlogged packets just before ith
  arrival.
• tj time interval from end of (j-1) successful
  transmission to end of jth success.
• yi time until beginning of next successful
  transmission after those ni transmissions.
• For each interval tj, backlog is at least two
  (i.e., ni ith arrival)
• Thus each slot is successful with probability
  1/e.
• (Assume that Psucc 1/e for n ? 2 and Psucc 1
  for n1)

23

24
delay
25
Splitting Algorithms

• Most often collision is between two users.
• It is advantageous to inhibit new arrivals from
  transmission until a collision is resolved.
• To resolve a collision, each node involved in
  the collision would retransmit in the next
• slot with probability 1/2.
• Collision is resolved in
• Two slots with probability 1/2.
• Three slots with probability 1/4.
• Four slots with probability 1/8.
• i slot with probability 2-(i-1).
• Expected number of slots for sending two packets
  equals 3
• throughout for this period 2/3.
• In essence, the set of colliding nodes are split
  into two sets those that transmit
• in the next slot and those that do not.
• Splitting Algorithms

26
Tree Algorithm

• Splitting algorithm has a tree structure when
  collision occurs.
• All nodes not involved in collision go into
  waiting mode.
• The first subnet transmits in the next slot.
• If this transmission is successful or idle, the
  second subject transmits in the following slot.
• If collision occurs in the retransmission, then
  the subset is split and so on.

LRRL success
success LRRR
idle LRL

• Mechanics
• A counter is set to 0 or 1 at the beginning of a
  collision for each packet.
• If it is 0, packet is transmitted.
• If it is non zero, it is incremented by 1 for
  each collision, and decreased by 1 for each
  success or idle.

collision
LRR
success
collision
LL
LR
idle
collision
R
L
collision
27
Issue

• What do we do with packets that arrived while
  collision was being resolved?
• A Collision Resolution Period (CRP) starts as
  soon as one ends. If many packets arrived in the
  meantime, they will collide immediately and have
  to be split and so on.
• Solution At the end of a CRP, split the set of
  nodes with new arrivals into j subjects with j
  such that the expected number of packets in each
  subsets is slightly larger than 1.
• These new packets are now transmitted via a tree
  structure.
• Maximum throughput for optimized j 0.43 packets
  per slot.

28
Improvement for Tree Algorithm

• The splitting at node A creates two subsets one
  of which is empty (i.e, left subset).
• This causes another collision in the next time
  slot (at right subset).
• 1st Improvement
• Omit transmission of the 2nd subset after an idle
  time slot, preceded by a collision. Split the 2nd
  subset before transmission. Throughput 0.46
  packets per slot

idle
collision
success
collision
collision
node A
idle
collision
29
2nd Improvement

• Suppose one collision follows another. Let
• x number of packets in the first collision
• xr number of packets in the right subset
• xl number of packets in the left subset
• Assume x xr xl is Poisson.

2nd Improvement When there is a collision,
regard the 2nd subset as new arrivals that have
not been involved in collision previously.
30
Unslotted Aloha

• There is no slot for timing.
• Packets are transmitted as they arrive.
• Collided packets are re-transmitted a random
  time later.
• Assume infinite number of nodes (6b Assumption).
• Let ? time until attempted retransmission.
• Suppose ? is exponential with probability density
  function xe-?x where x is node retransmission
  attempt rate.
• Let ? overall Poisson arrival rate.
• If n nodes are backlogged, there is also an
  arrival of rate nx from backlogged nodes
• which we assume to be Poisson.
• Total attempted transmission is Poisson with rate
  G(n) ? nx.

31
Let ?i duration of interval between ith and
(i1)st transmissions. The ith transmission is
successful if ti-1 gt 1 and ti gt 1.
32

• Maximum throughput 1/2e at G1/2.
• Pure Aloha (i.e., Unslotted Aloha) is unstable.

33
Carrier Sensing Multi Access (CSMA)

• In some multi-access systems, a node can hear
  when other nodes are transmitting.
• Detection is possible after a propagating and
  detection delay which is small compared to
• packet transmission time.
• Detection delay is the time it takes for the
  node to determine if other nodes are
  transmitting.
• ? propagation and detection delay in seconds
• C bits per second rate in the channel
• L average number of bits per packet
• Feedback is not instantaneous, but it is with a
  maximum delay of ß in packet transmission
• unit.
• If a slot is idle, then the slot terminates
  after ß time units and a new slot begins.
• ? ? ?C/L
• Slots are not of equal length.
• Idle slots have length ?.
• Other slots have length 1.

34
CSMA Slotted Aloha

• Idle slot duration ?
• If a packet arrives at a node while a
  transmission is in progress in the channel (by
  any node), the packet is regarded as backlogged.
• Backlogged packets begin transmission with
  probability qr after each subsequent idle slot.
• Non Persistent CSMA Packets arriving during
  idle slots are transmitted in the next slot
• Persistent CSMA All arrivals during a busy
  period transmit at the end of that slot.
• P-Persistent CSMA Collided packets and new
  packets use different probabilities for
  transmission.

35
Analysis of CSMA Slotted Aloha

• Each busy slot (success or collision) is
  followed by an idle slot.
• Node can only transmit after an idle slot.
• We want to evaluate the maximum throughput such
  that the drift is negative.
• Drift ? Dn
• expected number of arrivals
  expected number of departures
• E(number of arrivals) Psucc
• Define
• State number of backlogged packets
• State transition time end of idle slot
• We want to evaluate the drift at the state
  transition times.
• Time between state transitions
• ? if the slot is idle
• 1 ? if a busy slot is followed by idle
  slot

36

• Suppose the system is in state n.

Expected number of departures between state
transitions from state n where
37
(No Transcript)
38

• CSMA Slotted Aloha is unstable.
• It can be stabilized for all rates
  .
• Stability is not as a severe problem as in
  ordinary Aloha
• Expected idle time a backlogged node must wait
  before transmission is ?/qr as oppose to 1/qr
  for ordinary aloha.
• For small ? ,qr can be very small without
  causing much delay.
• n must very large before backlog appears.

39
Satellite Reservation Systems
Amv

• Round trip delay 2?
• Duration of reservation slot v
• Reservation period A mv
• 2? is many times larger than A.
• TDM is used to make reservations.
• Duration of data packet has general distribution
  with mean and second moment

1 2 m
reservation interval
Data intervals
arrival
res data res data res data
Wait for reservation
Wait for assigned data slot
40
Delay Analysis of Satellite Reservation System

• Consider the ith packet arriving into system.
• The ith packet must wait for
• residual time Ri (for the transmission or
  reservation currently in progress),
• transmission time of Ni packets already in
  queue for which reservations have been made
• two reservation periods.

41

• Satellite reservation system is an M/G/1 queue
  with vacation where reservations correspond to
  vacations.

42

• As v ? 0, the same queuing delay as M/G/1.
• W is finite for ? lt1.
• Every packet must be delayed by at lest 2? (gtgtA)
  in order for the reservations to be made.
• We need W gt 2?. ? This formula is only valid
  for ? ? 1.
• NoteThe use of variable frame size is
  undesirable.
• If the frame length is variable, errors made
  during a reservation period requires
  resynchronization on the next reservation period.
  This is not easy.
• Busy nodes can lock out less frequent nodes.
• ? Fixed frame length should be used.
• Since all nodes are aware of all reservations,
  any queuing discipline can be used as long as
• a packet is sent whenever the queue (which is
  common) is not empty.

43
Approximate Analysis of Delay

• Consider the following scheme
• A fraction ? of bandwidth is set aside for making
  reservations.
• TDM is used within this bandwidth.
• Each node gets one reservation slot in each round
  trip delay which is 2?.

44

• The arrival process of packets (with
  reservations) to the common queue is
  approximately
• Poisson.
• Number of arrivals in different reservation
  slots are independent and have Poisson
• distribution.
• A packet in common queue has the service time
• Where is the service time with full
  bandwidth.
• The common queue is M/G/1 with

data data
1-r
1 2 3 m
r
frame
45

• Assume
• The total queuing delay
• For small ?, large and needless delay for making
  reservation takes place.
• To reduce the number of data slots wasted in
  each frame, use an unscheduled contention
• mode. If a packet gets through before the
  reservation time, cancel its reservation.

46
Local Area networks Ethernet
nodes

• Model
• Propagation delay is very small.
• Nodes are connected to a common cable.
• When one node transmits all other nodes (which
  are silent) can hear that transmission.
• It is possible for a node to listen while
  transmitting.
• If two nodes start transmit almost
  simultaneously, they will shortly detect a
  collision and
• stop transmitting (CSMA/CD).
• If one node starts transmission and during the
  propagation delay and no other node starts
• transmission, then no other node will start
  transmission and the node transmitting is
  guaranteed the transmission without collision.

Ethernet cable
47
Slotted CSMA/CD

• Visualize Ethernet in terms of slots and
  mini-slots.
• ? Slots have duration of 1.
• ? Mini-slots have duration of ?.
• ? ? is the maximum propagation delay time in
  slot unit.
• Nodes are synchronized into mini-slots.
• If only one node starts transmitting, the other
  nodes can hear and will not transmit until
• the transmitting node has finished the
  transmission.
• If two nodes or more start transmission, they
  will detect a collision by the end of the
• mini-slot and both will stop transmission.
• Mini-slots are used in a contention mode and
  when a successful transmission occurs,
• the transmitting node reserves the channel
  for the slot for the completion of the packet.

48
Analysis

• Assumptions
• Each backlogged node will transmit with
  probability qr after an idle mini-slot.
• n number of backlogged node.
• Number of nodes transmitting after an idle slot
  is Poisson with parameter G(n) ?? nqr
• Consider state transitions after each idle
  mini-slot.
• No transmission idle slot ends after ? .
• One transmission next idle slot ends after 1?
  .
• More than one transmission next slot ends
  after 2?.

idle
idle
?
?
State transition
Packet transmission
idle
idle
1
?
?
State transition
idle
idle
idle
?
?
?
State transition
State transition
49

• Like Slotted Aloha

50

• ? is usually very small in LAN.
• It is very difficult to synchronize all nodes on
  short mini-slots
• Unslotted CSMA/CD makes more sense.

51
Token Ring
1
nodes
9
2
Interface units
3
8
4
7
5
6
52

• A collection of ring interfaces are connected in
  a ring topology.
• Nodes are connected to the ring through the
  interfaces. Token ring is more like a collection
  of point-to-point links.
• There is uni-directional transmission around the
  ring.
• Each bit arriving at an interface is copied into
  a one-bit buffer and then copied out into the
  ring again.
• The arrived bit can be inspected and modified
  before being written out.
• There is a one-bit delay at each interface.

53
Model

• A special bit pattern called token circulates
  around the ring whenever all nodes are idle.
• Token can be a flag indicating the end of
  packets, e.g., 01111110. (We need bit stuffing.)
• A node that does not have any packet to transmit
  simply passes the token to the next
• node with one bit delay.
• When a node wants to transmit, it seizes the
  token and inverts the last bit of the token
• and transmits. The token now becomes
  01111111 (i.e., busy token). After this busy
  token, the packet follows.
• Since there is only one token, the channel
  access problem is resolved.
• Ring interface has two modes
• Listen
• Transmit
• If the packet length is longer than the round
  trip delay, then when the busy token bits
• propagated around the ring, they are removed
  from the ring.
• IEEE 802.5 Standard 24 bit token, 4 or 10 Mbps

54
Notes

• Ring is susceptible to failures
• Ring breaks down if cable or any interface
  breaks down.
• Use a star configuration.
• Nodes can be by passed or added from the central
  site

55
Delay Analysis

• Assumptions
• This is called the exhaustive multi user
  reservation system.

56

• If each node can only transmit one packet at a
  time, then,
• This is called the partially gated multi user
  reservation system.

57
Fiber Distributed Data Interface(FDDI)
2 fiber rings
58

• Defined by American National Standard Institute
  (ANSI)
• Dual ring is constructed on optical fibers.
• Transmission rate 100Mbps.
• Uses 4 bits to 5 bits encoding.
• A group of 4 bits is encoded into a character
  which is 5 bits long.
• 16 characters represent 4 bits of data each.
• Other characters are special communication or
  control characters.
• 5-bit long characters contain at most 2
  successive 0s.
• To provide guaranteed service for high priority
  traffic (e.g., digitalized speech, video),
• we need to impose constraints on traffic.
• Question How much of high priority traffic can
  each node send per received token?

59
Model

• There are m nodes labeled as 0,1,2,,m-1.
• ?i for i 0,1,2,, m-1, is the amount of time
  node i can send high priority traffic, including
  delay to reach the next node.
• If a token is received at time t by node i, and
  node i sends ?i high priority traffic, and token
  reaches node i1 at t ?i.
• When the ring is initialized, there is a
  parameter ?, called target token rotation time.
• ? is used by nodes in deciding when to send low
  priority traffic.
• ? is the upper bound on the time average
  inter-token arrival time.

60
Distributed Queue Dual Bus (DQDB)
bus A

• Standardized as IEEE 802.6
• There are two buses running.
• Uses 53 byte long ATM frames.
• Frames contain two special bits.
• Busy bit B
• Request bit R
• B 1 if frame is busy.
• B 0 if frame is idle.
• Slots are used.
• Left most node on bus A generates slots for
  transmission on bus A.
• Right most node on bus B generates slots for
  transmission on bus B.

nodes
bus B
61
Packet Radio Networks

• This is a multiple access network where not all
  nodes can hear transmissions of other nodes.
• Network topology is represented by a graph
  containing nodes and links.
• Nodes are the sources and destinations of
  packets.
• Links are ordered pair of nodes (i, j) indicating
  transmission from i can be heard at j.
• Packets from i will be correctly received by j if
• There is a link between i and j.
• j or js neighbors are not transmitting.
• In the above diagram, if nodes 2 and 3 are
  transmitting simultaneously, nodes 1 and 5 will
  receive correctly, but node 6 will not.
• More links does not necessarily imply greater
  throughput.

62

• Definition Collision Free Set is a set of links
  that can carry packet simultaneously
• without collision at the end of the link.
• Example) In the previous diagram, (1,2), (4,5),
  (4,6) and (2,1),(5,3),(5,4) are collision free
  sets.
• Definition Collision Free Vector (CFV) is a
  vector of 0s and 1s where the ith component is
  1 iff the ith link is in the collision free set.
• (1,2) (2,1) (2,6) (3,5) (3,6) (4,5) (4,6) (5,3)
  (5,4) (6,2) (6,3) (6,4)
• 1 0 0 1 1 0
  0 0 0 0 0 0
• 1 0 0 0 0 1
  1 0 0 0 0 0
• 1 0 0 0 0 0
  0 1 1 0 0 0
• Once a collection of the collision free sets are
  known, we can assign a time slot for each set and
  cycle through like TDM. In the ith slot of TDM,
  all links in the ith collision free set can carry
  packets.

63

• f is a convex combination of CFVs.
• Any convex combination can be achieved by TDM.
• Any link utilization achievable by other
  allocation algorithms (e.g., collision resolution
  algorithms) can be achieved by TDM.
• TDM has an issue of long delay.
• A more difficult problem with TDM is for
  dynamic networks (i.e., one with changing
  topology like mobile networks).
• FDM can be used in stead of TDM.

64
Collision Resolution (Aloha)

• When an unbacklogged node receives a packet to
  transmit (from outside or other nodes),
• it sends the packets in the next slot.
• If no acknowledgement is received within a time
  out period, the node is backlogged and
• will retransmit after a random time.
• Consider heavy loading

65

• We can get through from qij.
• In design, we have a set of desired throughputs
  and want to find qij.
• Suppose fs are the desired throughputs.
• Algorithm for design