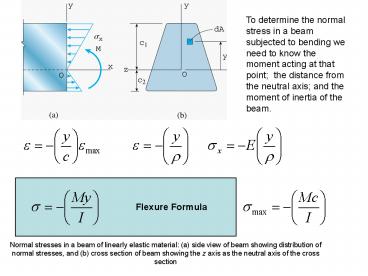
Normal stresses in a beam of linearly elastic material: (a) side view of beam showing distribution of normal stresses, and (b) cross section of beam showing the z axis as the neutral axis of the cross section

1
Normal stresses in a beam of linearly elastic
material (a) side view of beam showing
distribution of normal stresses, and (b) cross
section of beam showing the z axis as the neutral
axis of the cross section
To determine the normal stress in a beam
subjected to bending we need to know the moment
acting at that point the distance from the
neutral axis and the moment of inertia of the
beam.
Flexure Formula
2
Positive curvature results from positive applied
moments. For positive curvature compression
occurs at the top surface. The beams shown have
non-symmetric cross-sections and the neutral axis
is therefore not at the center.
3
Taking moments about the neutral z-axis (for each
small slice the force is stress x area and the
distance from the z-axis is y)
Remember
4
Doubly symmetric cross-sectional shapesIf a
beam is doubly symmetric (i.e. symmetric in the z
and y directions, the neutral axis will be at the
center of the beam.
Where Ssection modulus and is a geometric
factor. For beam design we can calculate the
required section modulus and then select.
5
FIG. 5-13 Example 5-2.Wire bent around a drum
O
6

• For the beam shown determine the maximum tensile
  and compressive stresses in the beam.
• Calculate the maximum ve and ve moments
• Need to draw shear and moment diagrams
• Mpos2.025 kN.m Mneg-3.6 kN.m
• 2) Find neutral axis

7
3) Find moment of inertia about the neutral
axis
8
3) Calculate the maximum ve and ve stresses
there are four combinations Mpos c1 Mpos c2
Mneg c1 Mneg c2
Tensile
Compressive
9
(No Transcript)
10
(No Transcript)
11
(No Transcript)
12
(No Transcript)
13
(No Transcript)
14
(No Transcript)
15
(No Transcript)
16
(No Transcript)
17
(No Transcript)
18
(No Transcript)
19
A simple beam of span length 21 ft must support a
uniform load q2000lb/ft as shown. Neglecting
the weight of the beam select a structural beam
of wide flange shape to support the loads.1)
Determine Mmax Draw shear diagram Calculate
M2) Calculate required section
modulus Calculate or look up max stress3)
Select a beam W12x50 S64.7
X19430 ft Mmax88,920 lb-ft SminMmax/?allow59.3
in3
Design of Beams
20
A cantilever beam AB of length L is being
designed to support a concentrated load at the
free end . The cross-section is rectangular.
Calculate the height as a function of distance so
that the beam is fully stressed. I.e. at every
point ??allow