Electromagnetic Induction

1
Electromagnetic Induction

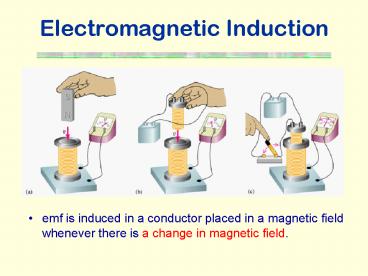
• emf is induced in a conductor placed in a
  magnetic field whenever there is a change in
  magnetic field.

2
Faradays work

• Faraday suggested that an e.m.f. is induced in a
  conductor when
• 1. there is a change in the number of lines
  linking it,
• 2. it cuts across field lines.

3

• As shown in the figure, if the coil moves towards
  the magnet from X to Y, the number of magnetic
  field lines linking it increases from three to
  five alternatively we can say it cuts two lines
  in moving from X to Y.
• Hence, an e.m.f. is induced in the coil.

4

• The figure shows two stationary coils A and B.
• When a current flowing in coil A increases or
  decreases, the magnetic flux linking coil B
  increases and decreases respectively. Hence, an
  e.m.f. is induced in coil B.

5
Magnetic flux

• B magnetic flux density (i.e. the number of
  magnetic field lines per unit cross-section area)
  
• A cross-section area,
• magnetic flux linking the area is the product BA
  represents the number of field lines linking a
  surface of cross-sectional area A.
• ? BA
• If B 1 T and A 1 m2, F is defined to be 1
  (Tm2) or weber (Wb).

6
Magnetic flux

• If the surface is not perpendicular to the field
  with the normal to the surface making an angle q
  to the field, the magnetic flux linking the area
  is ? BA cos q.
• If F is the flux through the cross-section area A
  of a coil of N turns, the total flux through it,
  called the flux-linkage, is NF since the same
  flux F links each of the N turns.

7
Example 1

• A circular coil of 20 turns with diameter 10 cm
  is placed in a region of uniform magnetic field
  of 1.5 T. Find the flux-linkage if the plane of
  the coil
• (a) is perpendicular to the field,
• Solution

8
Example 1

• A circular coil of 20 turns with diameter 10 cm
  is placed in a region of uniform magnetic field
  of 1.5 T. Find the flux-linkage if the plane of
  the coil
• (b) is along the field, and
• Solution

9
Example 1

• A circular coil of 20 turns with diameter 10 cm
  is placed in a region of uniform magnetic field
  of 1.5 T. Find the flux-linkage if the plane of
  the coil
• (c) makes an angle of 30o to the field.
• Solution

10
Faradays law
The induced e.m.f. is directly proportional to
the rate of change of flux-linkage or rate of
flux cutting.

• Mathematically, or
  .
• It is defined that 1 Wb is magnetic flux that
  induces in a one-turn coil an e.m.f. of 1 volt
  when the flux is reduced to zero in 1 s.
• By putting e 1 V, dt 1 s and d(NF) 1 Wb, we
  have 1 constant x 1/1.
• Hence,

11
Example 2

• (a) Suppose a 5000-turn coil of cross-section
  area 5 cm2 is at right angles to a flux density
  of 0.2 T, which is then reduced steadily to zero
  in 10 s. Find the e.m.f. induced in the coil.
• (b) Find the e.m.f. induced if the normal to the
  plane of coil makes an angle of 60o with the
  field.
• Solution

12
Lenzs law
13
Lenz's law
Induced I always flows to oppose the movement
which started it.
In both cases, magnet moves against a force.
Work is done during the motion it is
transferred as electrical energy.
14

• Lenzs law is incorporated in the mathematic
  expression of Faradays law by including a
  negative sign to show that current due to the
  induced e.m.f. produces an opposing flux change.
  So we have

15
Fleming's right-hand rule
For a wire cutting through a B-field...
motion or force F
magnetic field B
induced current I
16
Example 3

• State the direction of induced current flowing
  through coil B observed by the observer when the
  current through coil A increases steadily.
• Solution

17
Calculation of e.m.f.

• Consider a conducting rod of length l moving
  sideways with constant velocity v through and at
  right angles to a uniform magnetic field of flux
  density B.
• Area swept out per second by the rod per second
  lv
• Flux cut per second Blv
• e.m.f induced rate of flux-cutting flux cut
  per second
• e Blv

18
Alternative derivation

• Magnetic force Bqv.
• An electric field is built up due to the
  accumulation of charges.
• Electric force qE
• Finally, equilibrium is reached when magnetic
  force acting on electrons is balanced by electric
  force.
• Hence, qE Bqv ? E Bv
• An e.m.f. e is generated across the conductor
  such that
• e El Blv.

19
Example 4

• A metal aircraft of wing span l 32 m is flying
  with speed v 190 ms-1 towards the earths
  magnetic north pole in a region where the earths
  magnetic field BR 4.3 x 10-5 T and the angle of
  dip a 65o.
• Calculate the e.m.f. induced across its wing
  tips.
• Solution

20
Simple a.c. Generator

• According to the Faradays law of electromagnetic
  induction,

http//www.walter-fendt.de/ph11e/generator_e.htm
21
Simple d.c. Generator
22
Back e.m.f. Sparks appear while opening a switch

• There is current flowing in the coil of the
  electromagnet in use.
• When the circuit is broken by opening the switch,
  the current starts to drop and the flux linkage
  through the coil of the electromagnet decreases
  suddenly.
• By Faradays law, a large induced e.m.f. would
  develop across the coil of the electromagnet so
  as to oppose the change.
• Sparks occur due to the discharge across the
  small gap of the switch.

23
DC motors

• A d.c. motor consists of a coil on an axle,
  carrying a d.c. current in a magnetic field.
• The coil experiences a couple as in a moving-coil
  galvanometer which makes it rotate.
• When its plane is perpendicular to the field, a
  split-ring commutator reverses the current in the
  coil and ensures that the couple continues to act
  in the same direction thereby maintaining the
  rotation.

24
Back emf in Motors

• When an electric motor is running, its armature
  windings are cutting through the magnetic field
  of the stator. Thus the motor is acting also as a
  generator.
• According to Lenz's Law, the induced voltage in
  the armature will oppose the applied voltage in
  the stator.
• This induced voltage is called back emf.

25
Back emf and Power
Multiplying by I, then

• So the mechanical power developed in motor

26
Variation of current as a motor is started
Larger load
Zero load

• As the coil rotates, the angular speed as well as
  the back emf increases and the current decreases
  until the motor reaches a steady state.

27
The need for a starting resistance in a motor

• When the motor is first switched on, ? 0.
• The initial current, IoV/R, very large if R is
  small.
• When the motor is running, the back emf
  increases, so the current decrease to its working
  value.
• To prevent the armature burning out under a high
  starting current, it is placed in series with a
  rheostat, whose resistance is decreases as the
  motor gathers speed.

28
Variation of current with the steady angular
speed of the coil in a motor

• The maximum speed of the motor occurs when the
  current in the motor is zero.

29
Eddy Current

• An eddy current is a swirling current set up in a
  conductor in response to a changing magnetic
  field.
• When the magnetic flux linkage through a
  conductor changes, an e.m.f. is induced in it.
• If the conductor is a lump of metal. These are
  known as Eddy Currents.

• Eddy currents may be quite large because of the
  low resistance of the paths they follow.

30
Consider a metallic sheet moving away from a
magnetic field.

• By Lenzs law, eddy currents must flow in a
  direction to oppose the motion of the sheet.
• Hence, eddy currents act as an effective brake to
  its motion.
• The mechanical work done is converted into
  internal energy of the sheet.

31
Applications1 Smooth Braking Device

• The eddy currents induced in the copper plate
  produce a strong braking effect on the plate
  which stops oscillating quickly.
• If the copper plate is replaced by one with
  slits, the induced eddy currents, which can only
  flow within the narrow teeth between the slits,
  are greatly reduced. This is because the
  resistance of the path which the eddy currents
  follow is increased.

32
Braking effect in moving-coil galvanometer

• As the core swings in a magnetic field, eddy
  currents are induced in it. Since the eddy
  currents flow in a direction to oppose the
  motion, unwanted oscillations are reduced.

33

• Ideal design of the core is to produce critical
  damping in which oscillation is just avoided.

34
Metal Detector

• A pulsing current is applied to the coil, which
  then induces a magnetic field shown in blue. When
  the magnetic field of the coil moves across
  metal, such as the coin in this illustration, the
  field induces electric currents (called eddy
  currents) in the coin.
• The eddy currents induce their own magnetic
  field, shown in red, which generates an opposite
  current in the coil, which induces a signal
  indicating the presence of metal.
• A metal detector can also be used to detect mines
  buried underground.

35
Induction cooker

• The induction cooker uses coils of wire with high
  frequency a.c. to produce large eddy currents in
  the metal cooking pot placing above. The heating
  effect of the eddy current cooks the food.
• Moreover, since eddy current is not induced in
  its plastic case which is made up of non-metallic
  material, the cooker is not hot to touch.

36
Transformer

• A transformer is a device for stepping up or down
  an alternating voltage.
• For an ideal transformer,
• (i.e. zero resistance and no flux leakage)

37
Transformer Energy Losses

• Heat Losses
• Copper losses - Heating effect occurs in the
  copper coils by the current in them.
• Eddy current losses - Induced eddy currents flow
  in the soft iron core due to the flux changes in
  the metal.
• Magnetic Losses
• Hysteresis losses - The core dissipates energy on
  repeated magnetization.
• Flux leakage - Some magnetic flux does not pass
  through the iron core.

38
Designing a transformer to reduce power losses

• Thick copper wire of low resistance is used to
  reduce the heating effect (I2R).
• The iron core is laminated, the high resistance
  between the laminations reduces the eddy currents
  as well as the heat produced.
• The core is made of very soft iron, which is very
  easily magnetized and demagnetized.
• The core is designed for maximum linkage, common
  method is to wind the secondary coil on the top
  of the primary coil and the iron core must always
  form a closed loop of iron.

39
Transmission of Electrical Energy

• Wires must have a low resistance to reduce power
  loss.
• Electrical power must be transmitted at low
  currents to reduce power loss.
• To carry the same power at low current we must
  use a high voltage.
• To step up to a high voltage at the beginning of
  a transmission line and to step down to a low
  voltage again at the end we need transformers.

40
Direct Current Transmission

• Advantages
• a.c. produces alternating magnetic field which
  induces current in nearby wires and so reduce
  transmitted power this is absent in d.c.
• It is possible to transmit d.c. at a higher
  average voltage than a.c. since for d.c., the rms
  value equals the peak and breakdown of
  insulation or of air is determined by the peak
  voltage.
• Disadvantage
• Changing voltage with d.c. is more difficult and
  expensive.

41
Self Induction

• When a changing current passes through a coil or
  solenoid, a changing magnetic flux is produced
  inside the coil, and this in turn induces an emf.
  
• This emf opposes the change in flux and is called
  self-induced emf.
• The self-induced emf will be against the current
  if it is increasing.
• This phenomenon is called self-induction.

42
Definitions of Self-inductance (1)

• Definition used to find L

The magnetic flux linkage in a coil ? the current
flowing through the coil.
Where L is the constant of proportionality for
the coil. L is numerically equal to the flux
linkage of a circuit when unit current flows
through it.
Unit Wb A-1 or H (henry)
43
Definitions of Self-inductance (2)

• Definition that describes the behaviour of an
  inductor in a circuit

L is numerically equal to the emf induced in the
circuit when the current changes at the rate of
1 A in each second.
44
Inductors

• Coils designed to produce large self-induced emfs
  are called inductors (or chokes).
• In d.c. circuit, they are used to slow the growth
  of current.
• Circuit symbol

or
45
Inductance of a Solenoid

• Since the magnetic flux density due to a solenoid
  is

• By the Faradays law of electromagnetic induction,

46
Energy Stored in an Inductor

• The work done against the back emf in bringing
  the current from zero to a steady value Io is

47
Current growth in an RL circuit

• At t 0, the current is zero.
• So

• As the current grows, the p.d. across the
  resistor increases. So the self-induced emf (? -
  IR) falls hence the rate of growth of current
  falls.

• As t??

48
Decay of Current through an Inductor

• Time constant for RL circuit

• The time constant is the time for current to
  decrease to 1/e of its original value.

• The time constant is a measure of how quickly the
  current grows or decays.

49
emf across contacts at break

• To prevent sparking at the contacts of a switch
  in an inductive circuit, a capacitor is often
  connected across the switch.

The energy originally stored in the magnetic
field of the coil is now stored in the electric
field of the capacitor.
50
Switch Design

• An example of using a protection diode with a
  relay coil.

• A blocking diode parallel to the inductive coil
  is used to reduce the high back emf present
  across the contacts when the switch opens.

51
Non-Inductive Coil

• To minimize the self-inductance, the coils of
  resistance boxes are wound so as to set up
  extremely small magnetic fields.
• The wire is double-back on itself. Each part of
  the coil is then travelled by the same current in
  opposite directions and so the resultant magnetic
  field is negligible.