Remember Vector Algebra

1
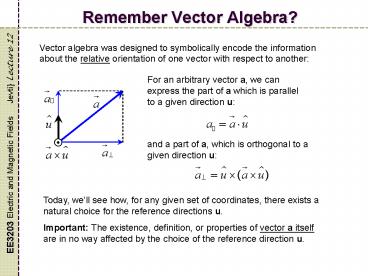
Remember Vector Algebra?
Vector algebra was designed to symbolically
encode the information about the relative
orientation of one vector with respect to
another
For an arbitrary vector a, we can express the
part of a which is parallel to a given direction
u
and a part of a, which is orthogonal to a given
direction u
Today, well see how, for any given set of
coordinates, there exists a natural choice for
the reference directions u. Important The
existence, definition, or properties of vector a
itself are in no way affected by the choice of
the reference direction u.
2
Consider Cartesian Coordinates
If the y coordinate of the point P(x,y,z) is
changed by dy, the point P is displaced to a new
point P(x,ydy,z). Think of PP as a vector
obtained by changing the y coordinate alone.
Clearly, vector PP points in the y-direction
Similarly for other 2 directions. We see that
this is a procedure that allows us to find the
local coordinate direction at any point of a
Cartesian system.
Can this line of reasoning be extended to
curvilinear coordinates?
3
Curvilinear Coordinates
Let us assign a set of three coordinates
to each point in space.
could be any of
,
Starting from a point P whose coordinates are
we obtain a new point P by an infinitesimal
change of only one of the coordinates, say
.
The vector
singles out a direction in space, at point P,
which well label as a unit vector

If this process is repeated for the other two
coordinates we obtain three unit vectors
which specify three directions at point
P.
The directions are called
coordinate induced basis and can be used as
reference directions for specifying an arbitrary
vector at the point P.
4
Prescription

• Given a) Coordinate system
• b) Point in space
• How to find the coordinate induced basis at the
  point?
• For each of 3 coordinates
• Increase the coordinate by an infinitesimal
  positive amount.
• See in which direction the point moves.
• Youve just found the induced direction for that
  coordinate.

5
Cartesian Coordinates
6
Cylindrical Coordinates
7
Spherical Coordinates
8
Summary
Spherical
Cylindrical
Cartesian
Coordinates
Basis vectors
Lamé coefficients