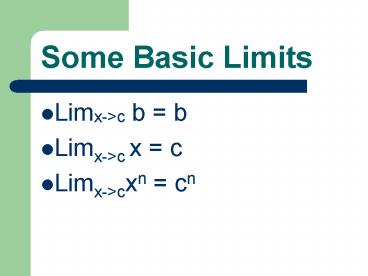Some Basic Limits PowerPoint PPT Presentation
Title: Some Basic Limits
1
Some Basic Limits
- Limx-gtc b b
- Limx-gtc x c
- Limx-gtcxn cn
2
Properties of Limits
- Let b and c be real numbers, n a positive
integer, and F and G functions so that - Limx-gtcF(X) L and
- Limx-gtcG(x) K.
3
Then
- Limx-gtcbF(x) bL
- Limx-gtcF(x) ? G(x) L ? K
- Limx-gtcF(x)G(x) LK
- Limx-gtc F(x)/G(X) L/K, if K ? 0
- Limx-gtc F(x)n Ln
4
Two more Properties
- If p(x) is a polynomial, then limx-gtcp(x) p(c).
- If r(x) p(x)/q(x) is a rational function and
q(c) ? 0, then limx-gtcp(x)/q(x) p(c)/q(c).
5
Composite Functions
- If F and G are functions so that limx-gtcG(x) L
and limx-gtc F(x) F(L) then - limx-gtc F(G(x)) F(L)
6
Trigonometric Functions
- Limx-gtc sin(x) sin(c)
- Limx-gtc cos(x) cos(c)
- Limx-gtc tan(x) tan(c)
- Limx-gtc cot(x) cot(c)
- Limx-gtc sec(x) sec(c)
- Limx-gtc csc(x) csc(c)
7
Another Limit Theorem
- If F(X) G(X) for all x? c in an open interval
containing c , then if both F(x) and G(X) have a
limit as x approaches c, then
Limx-gtcF(x) Limx-gtc G(x).
8
The Squeeze Theorem
- If H(x) lt F(x) lt G(x) for all x in an open
interval containing c, except possibly at c
itself, and if Limx-gtc H(x) Limx-gtc G(x) L,
then Limx-gtc F(x) L.
9
Two Important Trigonometric Limits
- Limx-gt0 sin(x)/x 1
- Limx-gt0 (1 cos(x)/x 0
PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.
You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.
About the Developers
PowerShow.com is brought to you by CrystalGraphics, the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.