Frequency Response

1
Chapter 14 Frequency Response
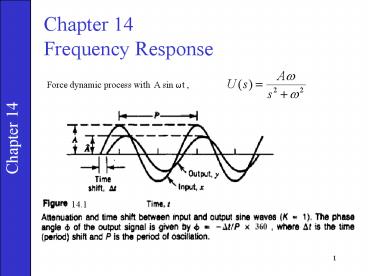
Force dynamic process with A sin ?t ,
Chapter 14
14.1
2
Input Output is the normalized
amplitude ratio (AR) ? is the phase angle,
response angle (RA) AR and ? are functions of
? Assume G(s) known and let
Chapter 14
3
Example 14.1
Chapter 14
K1 K2
4
Chapter 14
5
Use a Bode plot to illustrate frequency response
(plot of log G vs. log ? and ? vs. log ?)
log coordinates
Chapter 14
6
Chapter 14
Figure 14.4 Bode diagram for a time delay, e-qs.
7
Example 14.3
Chapter 14
8
F.R. Characteristics of Controllers
Recall that the F.R. is characterized by 1.
Amplitude Ratio (AR) 2. Phase Angle (?)
For any T.F., G(s)
A) Proportional Controller
Chapter 14
B) PI Controller
For
The Bode plot for a PI controller is shown in
next slide. Note ?b 1/?I . Asymptotic slope
(?? 0) is -1 on log-log plot.
9
Chapter 14
10
Ideal PID Controller.
Series PID Controller. The simplest version of
the series PID controller is
Chapter 14
Series PID Controller with a Derivative Filter.
The series controller with a derivative filter
was described in Chapter 8
11
Figure 14.6 Bode plots of ideal parallel PID
controller and series PID controller with
derivative filter (a 1). Ideal
parallel Series with Derivative Filter

Chapter 14
12
Advantages of FR Analysis for Controller
Design 1. Applicable to dynamic model of any
order (including non-polynomials). 2. Designer
can specify desired closed-loop response
characteristics. 3. Information on stability
and sensitivity/robustness is provided. Disadvant
age The approach tends to be iterative and hence
time-consuming -- interactive computer graphics
desirable (MATLAB)
Chapter 14
13
Controller Design by Frequency Response -
Stability Margins

• Analyze GOL(s) GCGVGPGM (open loop gain)
• Three methods in use
• (1) Bode plot G, ? vs. ? (open loop F.R.) -
  Chapter 14
• Nyquist plot - polar plot of G(j?) - Appendix J
• Nichols chart G, ? vs. G/(1G) (closed loop
  F.R.) - Appendix J
• Advantages
• do not need to compute roots of characteristic
  equation
• can be applied to time delay systems
• can identify stability margin, i.e., how close
  you are to instability.

Chapter 14
14
Chapter 14
14.8
15

• Frequency Response Stability Criteria
• Two principal results
• 1. Bode Stability Criterion
• 2. Nyquist Stability Criterion
• I) Bode stability criterion
• A closed-loop system is unstable if the FR of the
  
• open-loop T.F. GOLGCGPGVGM, has an amplitude
  ratio
• greater than one at the critical frequency,
  . Otherwise
• the closed-loop system is stable.
• Note where the
  open-loop phase angle
• is -1800. Thus,
• The Bode Stability Criterion provides info on
  closed-loop

Chapter 14
16
Example 1
A process has a T.F.,
And GV 0.1, GM 10 . If proportional control
is used, determine closed-loop stability for 3
values of Kc 1, 4, and 20.
Solution
Chapter 14
The OLTF is GOLGCGPGVGM or...
The Bode plots for the 3 values of Kc shown in
Fig. 14.9. Note the phase angle curves are
identical. From the Bode diagram
17
Chapter 14
Figure 14.9 Bode plots for GOL 2Kc/(0.5s 1)3.
18

• For proportional-only control, the ultimate gain
  Kcu is defined to be the largest value of
  Kc that results in a stable closed-loop system.
• For proportional-only control, GOL KcG and G
  GvGpGm.

AROL(?)Kc ARG(?) (14-58)

• where ARG denotes the amplitude ratio of G.
• At the stability limit, ? ?c, AROL(?c) 1 and
  Kc Kcu.

Chapter 14
19
Example 14.7
Determine the closed-loop stability of the system,
Where GV 2.0, GM 0.25 and GC KC . Find
?C from the Bode Diagram. What is the maximum
value of Kc for a stable system?
Chapter 14
Solution
The Bode plot for Kc 1 is shown in Fig. 14.11.
Note that
20
Chapter 14
14.11
21

• Ultimate Gain and Ultimate Period
• Ultimate Gain KCU maximum value of KC
  that results in a
• stable closed-loop system when
  proportional-only
• control is used.
• Ultimate Period
• KCU can be determined from the OLFR when
• proportional-only control is used with KC 1.
  Thus
• Note First and second-order systems (without
  time delays)
• do not have a KCU value if the PID controller
  action is correct.

Chapter 14
22

• Gain and Phase Margins
• The gain margin (GM) and phase margin (PM)
  provide
• measures of how close a system is to a
  stability limit.
• Gain Margin
• Let AC AROL at ? ?C. Then the
  gain margin is
• defined as GM 1/AC
• According to the Bode Stability
  Criterion, GM gt1 ? stability
• Phase Margin
• Let ?g frequency at which AROL 1.0
  and the
• corresponding phase angle is ?g . The
  phase margin
• is defined as PM 180 ?g
• According to the Bode Stability
  Criterion, PM gt0 ? stability
• See Figure 14.12.

Chapter 14
23
Chapter 14
24
Rules of Thumb A well-designed FB control system
will have Closed-Loop FR Characteristics An
analysis of CLFR provides useful information
about control system performance and robustness.
Typical desired CLFR for disturbance and setpoint
changes and the corresponding step response are
shown in Appendix J.
Chapter 14
25
Chapter 14
Previous chapter
Next chapter