Strong Acid-Weak Base and Weak Acid - Strong Base

1
Strong Acid-Weak Base and Weak Acid - Strong Base
2
CH3COOH(aq) OH-(aq) -gt CH3COO-(aq) H2O(l)
Slow change in pH before equivalence point
solution is a buffer CH3COOH(aq)/CH3COO-(aq) At
halfway point HA A- pH pKa At
equivalence, pH determined by CH3COO-(aq)
3

• Changes in pH during a titration of a weak
  acid/base with a strong base/acid
• Halfway to the stoichiometric point, the pH pKa
  of the acid
• The pH is greater than 7 at the equivalence point
  of the titration of a weak acid and strong base
• The pH is less that 7 at the equivalence point of
  the titration of a weak base and strong acid
• Beyond the equivalence point, the excess strong
  acid or base will determine the pH of the solution

4
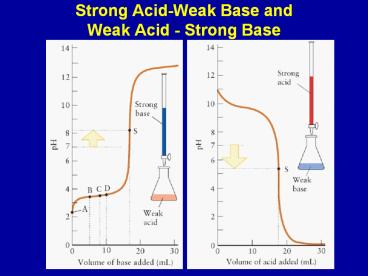
Titration of 100.0 mL of 0.1000 M CH3COOH(aq)
with 0.1000 M NaOH Before addition of NaOH pH
determined by CH3COOH(aq) CH3COOH(aq) H2O(l) ?
H3O(aq) CH3COO-(aq) Answer pH 2.88 Before
the equivalence point determine pH for a
buffer Addition of 30.00 mL of NaOH(aq) The
OH-(aq) reacts with the CH3COOH(aq). Determine
concentration of CH3COOH(aq) and CH3COO- (aq) in
solution after addition of the base. Answer pH
4.38 At half equivalence CH3COOH(aq)
CH3COO-(aq) pH pKa
5
At equivalence enough OH-(aq) added to react
with all CH3COOH(aq). For this problem,
equivalence is reached when 100.0mL of OH- is
added i.e. 0.01000 moles of OH-(aq) added
Solution contains 0.01000 moles CH3COO-(aq) in
200.0 mL solution CH3COO-(aq) 0.05000 M pH
determined by CH3COO-(aq) H2O(l) ? CH3COOH(aq)
OH- (aq) pH 8.72 (note greater than
7.0) Beyond equivalence pH determined by excess
OH-(aq)
6

• Estimate the pH at the equivalence point of the
  titration of 25.00 mL of 0.100 M HCOOH(aq) with
  0.150 M NaOH(aq)
• (Ka(HCOOH) 1.8 x 10-4)
• At the equivalence point, enough NaOH(aq) has
  been added to react with all the HCOOH(aq)
  forming HCOO-(aq)
• The reaction
• HCOO-(aq) H2O(l) ? HCOOH(aq) OH-
• determines the pH at equivalence
• Answer 8.26

7
Polyprotic acid and bases Titration of H2CO3 with
a strong base
8
Indicators

• A compound whose color changes noticeably over a
  short range of pH.

pH 7.0 8.5 9.4 9.8 12.0
9
(No Transcript)
10

• The indicator is a weak acid itself (HIn)
• HIn(aq) H2O(l) ? In- (aq) H3O (aq)

The acid form, HIn, has a different color from
the base form In- The end point of a titration is
the point at which the concentrations of the acid
and base forms of the indicator are equal
HIn(aq) In-(aq) Color change occurs when pH
pKIn
11

• In choosing an indicator
• pKIn pH(equivalence point) 1

12

• Applications
• Atmospheric CO2(g)
• CO2(g) H2O(l) ? H2CO3(aq)
• H2CO3(aq) H2O(l) ? HCO3-(aq) H3O(aq)
• Acid rain When pH lt 5.5
• due to pollutants in the air like SO2, SO3, NO2,
  which dissolve in water to form strong acids
• Many lakes have water too acidic to sustain life,
  forests have also been damaged.
• In the ground, acidic rain water can be
  neutralized by ions in the soil

13

• The ocean is buffered to a pH of 8.4 by buffering
  that depends on the presence of hydrogen
  carbonates and silicates
• Physiological Buffers
• Body fluids such as blood function over a very
  narrow pH range, maintained by buffers
• Blood contains two buffering systems
• 1) Phosphate buffer (H2PO4-/HPO42-)
• H2PO4-(aq) H2O(l) ? H3O(aq) HPO42-(aq)
• Ka2 6.2 x 10-8, pKa2 7.21
• Average pH of blood is 7.40 indicates that
• HPO42-(aq) / H2PO4-(aq) 1.55

14

• 2) HCO3-/H2CO3 buffer
• CO2(g) H2O(l) ? H2CO3(aq)
• H2CO3(aq) H2O(l) ? HCO3-(aq) H3O(aq)
  pKa1 6.36
• HCO3-(aq) / H2CO3(aq) 11.0
• Build up of H2CO3 would destroy this balance.
• In the body
• H2CO3(aq) ? H2O(l) CO2 (g)
• CO2 is exhaled from the lungs to prevent buildup
  of H2CO3

15
Solubility Equilibria

• Many ionic solids dissociate into their ions in
  water
• NaCl(aq) -gt Na(aq) Cl- (aq).
• Compounds such as NaCl exist completely as Na
  (aq) and Cl- (aq) in aqueous solutions unless the
  amount of NaCl exceeds the solubility of NaCl in
  water
• Other compounds such as CaCO3 dissolve to a very
  small extent in water - sparingly soluble

16
The Earths crust consists largely of sparingly
soluble salts e.g. gypsum (CaSO4.2H2O), calcite
(CaCO3), dolomite (xCaCO3.yMgCO3), oxides and
sulfides of metals such as Fe, aluminosilicates
(XAlSi3O8 or XAlSi2O8, X Na, K,
Ca2) Hard-water contains high levels of Ca2
and Mg2 Ca2 forms soap scum with detergents.
Add soluble Na2CO3 (washing soda) to precipitate
CaCO3 which washes off. Chemical weathering
includes the dissolving of sparingly soluble
salts. CaCO3(s) CO2(g) H2O(l) ? Ca2(aq) 2
HCO3-(aq)
17
Highly soluble compounds several grams of the
compound dissolves per 100 g of water At 298 K
36 g of NaCl, 122 g of AgNO3 Sparingly soluble
compounds less than one gram dissolves per 100 g
of water At 298 K 2.4 x 10-4 g of AgCl 9.3 x
10-4 g of CaCO3, 4.4 x 10-14 g of PbS
18

• AgCl(s) ? Ag (aq) Cl- (aq)
• Define an equilibrium constant for this process
  solubility product, Ksp

The solubility product, Ksp, is the equilibrium
constant for the equilibrium between an
undissolved salt and its ions in a saturated
solution.
19
(No Transcript)
20

• The molar solubility of Ag2Cr2O4 is 6.5 x 10-5
  mol/L at 25o C. Determine the value of Ksp.
• Ag2Cr2O4(s) ? 2 Ag (aq) Cr2O42- (aq)
• Ksp Ag (aq) 2 Cr2O42- (aq)
• Ag (aq) 2 x 6.5 x 10-5 mol/L
• Cr2O42- (aq) 6.5 x 10-5 mol/L
• Ksp 1.1 x 10-12

21
Determine the solubility of BaSO4(s) in pure
water at 298 K in moles/liter and grams/liter.
Ksp (BaSO4) 1.1 x 10-10 BaSO4(s) ? Ba2 (aq)
SO42- (aq) If x is the solubility in moles/liter
Ba2(aq) SO42-(aq) x2 1.1 x
10-10 Ba2(aq) SO42-(aq) 1.0 x 10-5
M Solubility of BaSO4 is 1.0 x 10-5 M or 2.3 x
10-3 g/L
22
Precipitation from Solution

• If equal volumes of aqueous solutions of 0.2 M
  Pb(NO3)2 and KI are mixed will PbI2(s)
  precipitate out? Ksp of PbI2 is 1.4 x 10-8
• Use the reaction quotient, Q, to predict whether
  precipitation will occur
• Pb(NO3)2 (aq) KI(aq) -gt PbI2 (s) KNO3 (aq)
• Net ionic equation Pb2 (aq) 2I- (aq) -gt PbI2
  (s)
• The reverse of this reaction defines Ksp
• PbI2 (s) ? Pb2 (aq) 2I- (aq)

23

• Ksp Pb2 (aq) I- (aq)2
• If Q gt Ksp precipitation if Q lt Ksp no
  precipitation
• Equal volumes of Pb(NO3)2 and KI are mixed
• On mixing, volume of mixed solution is twice
  initial volume
• Pb2 (aq) 0.2M / 2 0.1 M
• I- (aq) 0.1 M
• Q Pb2(aq) I- (aq)2 (0.1)(0.1)2 0.001
  M
• Q gt Ksp PbI2(s) precipitates