Introduction to NMR'

1
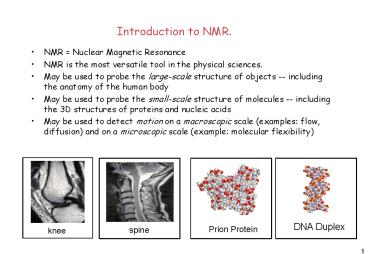
Introduction to NMR.

• NMR Nuclear Magnetic Resonance
• NMR is the most versatile tool in the physical
  sciences.
• May be used to probe the large-scale structure of
  objects -- including the anatomy of the human
  body
• May be used to probe the small-scale structure of
  molecules -- including the 3D structures of
  proteins and nucleic acids
• May be used to detect motion on a macroscopic
  scale (examples flow, diffusion) and on a
  microscopic scale (example molecular flexibility)

Prion Protein
2

• Why bother learning NMR?
• Structural (chemical) elucidation
• Natural product chemistry.
• Synthetic organic chemistry. Analytical tool of
  choice of
• synthetic chemists.
• Study of dynamic processes
• Reaction kinetics.
• Study of equilibrium (chemical or structural).
• Structural (three-dimensional) studies
• Proteins.
• DNA. Protein/DNA complexes

3
History of nuclear magnetic resonance

• 1946 Bloch, Purcell First nuclear magnetic
  resonance
• 1955 Solomon NOE (nuclear Overhauser effect)
• 1966 Ernst, Anderson Fourier transform NMR
• 1975 Jeener, Ernst Two-dimensional NMR
• 1985 Wüthrich First solution structure of a
  small protein
• NMR is about 25 years younger than X-ray
  crystallography
• 1987/8 3D NMR 13C, 15N isotope labeling
• 1996/7 New long-range structural parameters
  residual dipolar couplings (also
  anisotropic diffusion
• 2003 First solid state NMR structure of a
  small protein
• Nobel Prizes
• 1944 Physics Rabi (Columbia)
• 1952 Physics Bloch (Stanford), Purcell
  (Harvard)
• 1991 Chemistry Ernst (ETH)
• 2002 Chemistry Wuthrich (ETH)
• 2003 Medicine Lauterbur (Urbana), Mansfield
  (Nottingham)

4
History of Protein NMR

• NMR is a relatively new technique compared with
  x-ray
• X-ray structure of myoglobin (17.8 kDa) by John
  Kendrew, 1963
• Kendrew, J. C. (1963) Science 139, 1259-1266.
  Myoglobin and the structure of proteins.
• X-ray structure of hemoglobin (66 kDa) by Max
  Perutz, 1963
• Perutz, M. F. (1963) Science 140, 863-869.
  X-ray analysis of hemoglobin.
• NMR structure of proteinase inhibitor IIA (6
  kDa), 1985
• Williamson, M. P., Havel, T. F. and Wuthrich, K.
  (1985) J. Mol. Biol. 182, 295-315.
• Why did NMR take so long to evolve?

5

• Why study protein structure?
• The more we understand about a protein and its
  function, the more we can do with it. It can be
  used for a new specific purpose or even be
  redesigned too carry out new useful functions
  (biotechnology industry).
• We can use this knowledge to help understand the
  basis of diseases and to design new drugs
  (medicine drug design).
• The more knowledge we have how proteins behave
  in general, the more we can apply it to others
  (protein families etc)

Complex, could be the active form
6
Why biomolecular NMR?

• Structure determination of biomacromolecules
• no crystal needed, native like conditions
• nucleic acids difficult to crystallize,
  affected by crystal packing
• Ligand binding and molecular interactions in
  solution.
• - Bandshift in NMR fingerprint - with
  residue/amino acid resolution !!!
• Characterization of dynamics and mobility (ps to
  s)
• -conformational dynamics . enzyme turnover,
  kinetics, folding
• Molecular weight X-ray gt 200 kDa, NMR lt 50-100
  kDa
• - NMR and X-ray crystallography are complementary

7
(No Transcript)
8
Felix Bloch
Edward Purcell
9

• The more details
• Absorption (or emission) spectroscopy, as IR or
  UV. Detects
• the absorption of radiofrequencies
  (electromagnetic radiation)
• by certain nuclei in a molecule.
• Unfortunately, some quantum mechanics are needed
  to
• understand it (a lot to really understand it).
• Only nuclei with spin number (I) ? 0 can
  absorb/emit electro-
• magnetic radiation.
• Even atomic mass number ? I 0 (12C, 16O)
• Even atomic mass odd number ? I whole
  integer
• (14N, 2H, 10B)
• Odd atomic mass ? I half integer (1H, 13C,
  15N, 31P)
• The spin states of the nucleus (m) are
  quantified
• m I, (I - 1), (I - 2), , -I

10
(No Transcript)
11
(No Transcript)
12
(No Transcript)
13
(No Transcript)
14
(No Transcript)
15

• Background (continued)
• For 1H, 13C, 15N, 31P (biologically relevant
  nuclei) then
• m 1/2, -1/2
• This means that only two states (energy levels)
  can be
• taken by these nuclei.
• Another important parameter of each particular
  nuclei is
• the magnetic moment (m), which can be expressed
  as
• m g I h / 2p
• It is a vector quantity that gives the direction
  and magnitude
• (or strength) of the nuclear magnet
• h is the Planck constant
• g is the gyromagnetic ratio, and it depends on
  the

16

• Effect of a magnetic field (for I 1/2)
• In the ground state all nuclear spins are
  disordered, and there
• is no energy difference between them. They are
  degenerate
• Since they have a magnetic moment, when we apply
  a strong
• external magnetic field (Bo), they orient
  either against or with it

g h / 4p
Bo
17

• Energy and populations
• Upon application of the external magnetic field
  we create an
• energy difference between nuclei aligned and
  against Bo
• Each level has a different population (N), and
  the difference
• between the two is related to the energy
  difference by the
• Boltzmman distribution
• Na / Nb e DE / kT
• The DE for 1H at 400 MHz (Bo 9.5 T) is 3.8 x
  10-5 Kcal / mol

b
Bo gt 0
DE h n
a
Bo 0
18

• Energy and sensitivity
• The energy (for a single spin) is proportional
  to the magnetic
• moment of the nuclei and the external magnetic
  field
• E - m . Bo ? E(up) g h Bo / 4p ---
  E(down) - g h Bo / 4p
• DE g h Bo / 2p
• This has implications on the energy (i.e., the
  intensity of the
• signal and sensitivity) that each nuclei can
  absorb
• Bigger magnets (bigger Bo) make more sensitive
  NMR
• instruments.
• Nuclei with larger g absorb/emit more energy and
  are
• therefore more sensitive. Sensitivity is
  proportional to
• m, to Na - Nb, and to the coil magnetic flux,
  which are
• all dependent on g. Therefore, it is
  proportional to g3.

g13C 6,728 rad / G g1H 26,753 rad / G
1H is 64 times more sensitive than 13C just
because of the g
19
(No Transcript)
20
(No Transcript)
21
(No Transcript)
22
(No Transcript)
23
Gyromagnetic ratio (1)

• The gyromagnetic ratio g determines the ratio of
  the nuclear magnetic moment to the nuclear spin.
• It is a fundamental property of each nuclear
  isotope
• Fundamental symmetry theorems predict that spin
  and magnetic moment are co-linear

m
m gI
This equation tells us how much magnetism we get
for a given spin.
The gyromagnetic ratio is also known as the
magnetogyric ratio
24
Zeeman splitting

• Energy of interaction is given by E-m.B in a
  magnetic field B. The dot product tells us the
  energy depends on the size and relative
  orientation of B and m.

• We take Bo to be along the Z axis, so the dot
  product becomes E-mzBz(o) (I.e. mxBz and myBz
  0

• the energy of the state with quantum number Iz
  is given by

gyromagnetic ratio
Planck constant
25
I1/2
I1
m-1/2
m-1
m 0
m1/2
m1
ground state no field
Zeeman splitting h g B/2p
ground state with field
The Zeeman splitting is therefore
26
s-1 (Hz)
rad s-1
rad s-1 T-1
T
27
A compass in a magnetic field
28
A nuclear spin precesses in a magnetic field
the circulating motion of the spin angular
momentum is called precession
this arrow denotes the direction of the spin
angular momentum

• Nuclear spins precess because
• they are magnetic
• they have angular momentum

29
Precession frequency Larmor frequency
n0 - g Bo/2p
magnetic field in Tesla (T)
Larmor frequency in Hz ( cycles per second)
gyromagnetic ratio in rad s1 T1
Compare with Zeeman Splitting
30
Apply radio frequency to measure the nuclear
precession frequencies at
31
Nuclear Spin
NMR properties of selected nuclei
Nucleus I ????s)-1 rad ?rel Natural Abundance
() 1H 1/2 2.6752 x 108 1.00 99.98 2H 1 4.107 x
107 0.15 0.02 13C 1/2 6.728 x 107 0.25 1.11 14N 1
1.934 x 107 99.64 15N 1/2 -2.712 x
107 0.1 0.36 17O 5/2 -3.628 x 107 0.04 19F 1/2 2.
5181x107 100 23Na 3/2 7.080 x 107 100 31P 1/2 1.
0841 x 108 0.41 100 113Cd 1/2 5.934 x 107 12.26
The magnetic dipole moment ? and therefore the
precession frequency are characteristic for
each Nucleus and scale with the gyromagnetic
ratio.
Atomic nuclei are composed of protons and
neutrons which have a spin Protons spin
neutrons spin nuclear spin m Even even 0
0 Even odd 1/2 lt0 Odd even
1/2 gt0 Odd odd n gt0
32
Zeeman Levels
33
(No Transcript)
34
(No Transcript)
35
A one-dimensional (1D) NMR spectrum of a protein
H2O
Methyl
H?
HN
Backbone HN
H?
Aromatics
600.134800
600.132400
600.130000
2
9
3
1
0
8
7
6
5
4
Upfield shifted methyls
1H chemical shift (ppm)
Chemical shifts in parts per million (ppm) Are
independent of the field strength of the Static
magnetic Bo field. See the supplementary lecture
material and Rattle, NMR Primer for Life
Scientists Pages 19-21, 26.
36
Despite all this 1D NMR can provide some
information
1.) As we saw we can study the global
appearance of the 1D spectrum. 2.) It can be
very specific - we can monitor just one clearly
resolved signal - even if it is in a large
protein. 3.) It works in solution - can monitor
the effects of temperature, pH, buffer conditions
and stability over time.
37
Y215Q
38
(No Transcript)
39
(No Transcript)
40
(No Transcript)
41
(No Transcript)
42
(No Transcript)