Graph Algorithms: Shortest Path

1
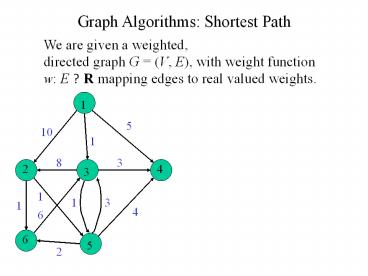
Graph Algorithms Shortest Path
We are given a weighted, directed graph G (V,
E), with weight function w E ? R mapping edges
to real valued weights.
1
5
10
1
3
8
2
4
3
1
3
1
1
4
6
6
5
2
2
Graph Algorithms Shortest Path
We are given a weighted, directed graph G (V,
E), with weight function w E ? R mapping edges
to real valued weights.
1
The weight of a path p (v , v , . . ., v
) is ? w(v , v ).
5
10
1
1
2
k
k-1
3
8
2
4
3
i
i1
i1
1
The weight of the path along the red edges is
1 6 1 4 12.
3
1
1
4
6
6
5
2
3
Graph Algorithms Shortest Path
We are given a weighted, directed graph G (V,
E), with weight function w E ? R mapping edges
to real valued weights.
1
The weight of a path p (v , v , . . ., v
) is ? w(v , v ).
5
10
1
1
2
k
k-1
3
8
2
4
3
i
i1
i1
1
Single source shortest path problem given a
vertex s, for every vertex v ? V find a shortest
path from s to v.
3
1
1
4
6
6
5
2
4
Graph Algorithms Shortest Path
Single source shortest path problem given vertex
s, for every vertex v ? V find a shortest path
from s to v.
1
5
10
1
Dijkstras algorithm solves this problem
efficiently for the case in which all weights
are nonnegative (as in the example graph).
3
8
2
4
3
1
3
1
1
4
6
6
5
2
5
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
1
It also maintains, for each vertex v not in S, an
upper bound dv on the weight of a shortest path
from source s to v.
5
10
1
3
8
2
4
3
1
3
1
1
4
6
6
5
2
6
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
1
It also maintains, for each vertex v not in S, an
upper bound dv on the weight of a shortest path
from source s to v.
5
10
1
3
8
2
4
3
1
The algorithm repeatedly selects the vertex u ? V
S with minimum bound dv, inserts u into
S, and relaxes all edges leaving u.
3
1
1
4
6
6
5
2
7
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
Set S initially.
5
10
1
v
2
3
4
5
6
1
3
8
2
4
3
d
?
?
?
0
?
?
1
3
1
1
4
6
Also initialize a queue with all the vertices and
their upper bounds.
6
5
2
8
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
S
5
10
1
v
2
3
4
5
6
1
3
8
2
4
3
d
?
?
?
0
?
?
1
Select the vertex u ? V S with minimum bound
dv, insert u into S, . . .
3
1
1
4
6
6
5
2
9
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
(here we keep the bound with the vertex in S)
1
S
5
0
10
1
v
2
3
4
5
6
3
8
2
4
3
d
?
?
?
?
?
. . . remove it from the queue, insert it in S,.
. .
1
3
1
1
4
6
6
5
2
10
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
1
S
5
0
10
1
v
2
3
4
5
6
3
8
2
4
10
1
5
?
?
3
d
. . . and relax the edges from this vertex.
1
3
1
1
4
6
6
5
2
11
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
1
S
5
0
10
1
v
2
3
4
5
6
3
8
2
4
10
1
5
?
?
3
d
. . . reordering the queue according to the new
upper bounds.
1
3
1
1
4
6
6
5
2
12
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
1
S
5
0
10
1
v
2
3
4
5
6
3
8
2
4
10
1
5
?
?
3
d
Repeat . . .
1
3
1
1
4
6
6
5
2
13
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
3
1
S
5
1
0
10
1
v
2
4
5
6
3
8
2
4
10
5
?
?
3
d
1
. . . remove from queue and put in S
3
1
1
4
6
6
5
2
14
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
3
1
S
5
1
0
10
1
v
2
4
5
6
3
8
2
4
9
4
2
?
3
d
1
. . . relax the edges . . .
3
1
1
4
6
6
5
2
15
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
3
1
S
5
1
0
10
1
v
2
4
5
6
3
8
2
4
9
4
3
2
?
d
1
. . . and reorder the queue . . .
3
1
1
4
6
6
5
2
16
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
3
1
S
5
1
0
10
1
v
2
4
5
6
3
8
2
4
9
4
3
2
?
d
Repeat . . .
1
3
1
1
4
6
6
5
2
17
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
5
3
1
S
5
1
2
0
10
1
v
2
4
6
3
8
2
4
9
4
3
?
d
1
. . . remove from queue and put in S
3
1
1
4
6
6
5
2
18
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
5
3
1
S
5
1
2
0
10
1
v
2
4
6
3
8
2
4
9
4
3
4
d
1
. . . relax the edges . . .
3
1
1
4
6
6
5
2
19
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
5
3
1
S
5
1
2
0
10
1
v
2
6
4
3
8
2
4
9
3
4
4
d
1
. . . and reorder the queue . . .
3
1
1
4
6
6
5
2
20
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
5
3
1
S
5
1
2
0
10
1
v
2
6
4
3
8
2
4
9
3
4
4
d
Repeat . . .
1
3
1
1
4
6
6
5
2
21
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
5
4
3
1
S
5
1
2
4
0
10
1
v
2
6
3
8
2
4
9
3
4
d
1
. . . remove from queue and put in S
3
1
1
4
6
6
5
2
22
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
5
4
3
1
S
5
1
2
4
0
10
1
v
2
6
3
8
2
4
9
3
4
d
1
. . . relax the edges (no change in this case) .
. .
3
1
1
4
6
6
5
2
23
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
5
4
3
1
S
5
1
2
4
0
10
1
v
2
6
3
8
2
4
3
9
4
d
1
. . . and reorder the queue (no change in this
case) . . .
3
1
1
4
6
6
5
2
24
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
1
5
4
3
1
S
5
1
2
4
0
10
1
v
2
6
3
8
2
4
3
9
4
d
Repeat . . .
1
3
1
1
4
6
6
5
2
25
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
6
1
5
4
3
1
S
5
1
2
4
0
4
10
1
v
2
3
8
2
4
3
9
d
1
. . . remove from queue and put in S
3
1
1
4
6
6
5
2
26
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
6
1
5
4
3
1
S
5
1
2
4
0
4
10
1
v
2
3
8
2
4
3
9
d
1
. . . relax the edges (no change in this case) .
. .
3
1
1
4
6
6
5
2
27
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
6
1
5
4
3
1
S
5
1
2
4
0
4
10
1
v
2
3
8
2
4
9
3
d
1
Repeat . . .
3
1
1
4
6
6
5
2
28
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
10
1
v
3
8
2
4
3
d
1
Done!
3
1
1
4
6
6
5
2
29
Graph Algorithms Shortest Path
Dijkstras algorithm maintains a set S of
vertices whose final shortest path weights have
already been determined.
Suppose vertex 1 is the source.
s
v
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
d
10
1
3
8
2
4
3
The result is the bottom row which contains the
length of the shortest path from s to the vertex
above it.
1
3
1
1
4
6
6
5
2
30
Graph Algorithms Shortest Path
s
v
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
d
10
1
5
p
3
3
3
1
3
8
2
4
3
To compute the corresponding paths, we augment
the data structure with an additional attribute,
p(v), which is the vertex that precedes v in
a shortest path.
1
3
1
1
4
6
6
5
2
31
Graph Algorithms Shortest Path
s
v
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
d
10
1
5
p
3
3
3
1
3
8
2
4
3
Using the predecessor attribute, p(v), its easy
to construct the path to v, working backwards
from v to s.
1
3
1
1
4
6
6
5
2
32
Graph Algorithms Shortest Path
s
v
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
d
10
1
5
p
3
3
3
1
3
8
2
4
3
E.g., v 6.
1
3
1
1
4
6
6
5
2
33
Graph Algorithms Shortest Path
s
v
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
d
10
1
5
p
3
3
3
1
3
8
2
4
3
E.g., v 6. p(6) 5,
1
3
1
1
4
6
6
5
2
34
Graph Algorithms Shortest Path
s
v
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
d
10
1
5
p
3
3
3
1
3
8
2
4
3
E.g., v 6. p(6) 5, p(5) 3,
1
3
1
1
4
6
6
5
2
35
Graph Algorithms Shortest Path
s
v
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
d
10
1
5
p
3
3
3
1
3
8
2
4
3
E.g., v 6. p(6) 5, p(5) 3, p(3)
1.
1
3
1
1
4
6
6
5
2
36
Graph Algorithms Shortest Path
s
v
6
1
2
5
4
3
1
S
1
5
9
2
4
4
0
d
10
1
5
p
3
3
3
1
3
8
2
4
3
E.g., v 6. p(6) 5, p(5) 3, p(3)
1.
1
3
1
1
4
6
6
5
Path 1, 3, 5, 6. Weight 4.
2
37
Graph Algorithms Shortest Path

• Computing time analysis look at different
  implementations
• of the priority queue, with different costs for
  the queue
• operations.
• Delete_min executed how many times?

38
Graph Algorithms Shortest Path

• Computing time analysis look at different
  implementations
• of the priority queue, with different costs for
  the queue
• operations.
• Delete_min executed V times.

39
Graph Algorithms Shortest Path

• Computing time analysis look at different
  implementations
• of the priority queue, with different costs for
  the queue
• operations.
• Delete_min executed V times.
• Decrease_key executed how many times?

40
Graph Algorithms Shortest Path

• Computing time analysis look at different
  implementations
• of the priority queue, with different costs for
  the queue
• operations.
• Delete_min executed V times.
• Decrease_key executed E times.
• Total time V T E T

Delete_min
Decrease_key
41
Graph Algorithms Shortest Path

• Computing time analysis look at different
  implementations
• of the priority queue, with different costs for
  the queue
• operations.
• Delete_min executed V times.
• Decrease_key executed E times.
• Total time V T E T

Delete_min
Decrease_key
Priority queue T T
Total time Array Binary
heap
Decrease_key
Delete_min
42
Graph Algorithms Shortest Path

• Computing time analysis look at different
  implementations
• of the priority queue, with different costs for
  the queue
• operations.
• Delete_min executed V times.
• Decrease_key executed E times.
• Total time V T E T

Delete_min
Decrease_key
Priority queue T T
Total time Array
O(V) O(1)
Binary heap
Decrease_key
Delete_min
43
Graph Algorithms Shortest Path

• Computing time analysis look at different
  implementations
• of the priority queue, with different costs for
  the queue
• operations.
• Delete_min executed V times.
• Decrease_key executed E times.
• Total time V T E T

Delete_min
Decrease_key
Priority queue T T
Total time Array
O(V) O(1)
O(V ) Binary heap O(log V)
O(log V)
Decrease_key
Delete_min
2
44
Graph Algorithms Shortest Path

• Computing time analysis look at different
  implementations
• of the priority queue, with different costs for
  the queue
• operations.
• Delete_min executed V times.
• Decrease_key executed E times.
• Total time V T E T

Delete_min
Decrease_key
Priority queue T T
Total time Unsorted Array
O(V) O(1)
O(V ) Binary heap O(log V)
O(log V) O(E log V)
Decrease_key
Delete_min
2