Continuous Probability Distributions

1
Continuous Probability Distributions

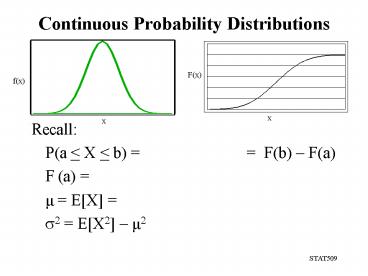
• Recall
• P(a lt X lt b) F(b)
  F(a)
• F (a)
• µ EX
• s2 EX2 µ2

F(x)
f(x)
x
x
2
Continuous Uniform Distribution

• f(xA,B) 1/(B-A), A lt x lt B
• where A,B is an interval on the real number
  line
• µ (A B)/2 and s2 (B-A)2/12

1/(B-A)
3
Continuous Uniform Distribution

• EX Let X be the uniform continuous random
  variable that denotes the current measured in a
  copper wire in milliamperes. 0 lt x lt 50 mA. The
  probability density function of X is uniform.
• f(x) , 0 lt x lt 50
• What is the probability that a measurement of
  current is between 20 and 30 mA?
• What is the expected current passing through the
  wire?
• What is the variance of the current passing
  through the wire?

4
Normal Distribution

• n(xµ,s)
• EX µ and VarX s2

f(x)
x
5
Normal Distribution

• Many phenomena in nature, industry and research
  follow this bell-shaped distribution.
• Physical measurements
• Rainfall studies
• Measurement error
• There are an infinite number of normal
  distributions, each with a specified µ and s.

6
Normal Distribution

• Characteristics
• Bell-shaped curve
• -? lt x lt ?
• µ determines distribution location and is the
  highest point on curve
• Curve is symmetric about µ
• s determines distribution spread
• Curve has its points of inflection at µ s
• µ 1s covers 68 of the distribution
• µ 2s covers 95 of the distribution
• µ 3s covers 99.7 of the distribution

7
Normal Distribution
s
s
s
s
µ


8
Normal Distribution
n(x µ 0, s 1)
n(x µ 5, s 1)
f(x)
x
9
Normal Distribution
n(x µ 0, s 0.5)
f(x)
n(x µ 0, s 1)
x
10
Normal Distribution
n(x µ 5, s .5)
f(x)
n(x µ 0, s 1)
x
11
Normal Distribution
µ 1s covers 68
µ 2s covers 95
µ 3s covers 99.7
12
Standard Normal Distribution

• The distribution of a normal random variable with
  mean 0 and variance 1 is called a standard normal
  distribution.

13
Standard Normal Distribution

• The letter Z is traditionally used to represent a
  standard normal random variable.
• z is used to represent a particular value of Z.
• The standard normal distribution has been
  tabularized.

14
Standard Normal Distribution

• Given a standard normal distribution, find the
  area under the curve
• (a) to the left of z -1.85
• (b) to the left of z 2.01
• (c) to the right of z 0.99
• (d) to right of z 1.50
• (e) between z -1.66 and z 0.58

15
Standard Normal Distribution

• Given a standard normal distribution, find the
  value of k such that
• (a) P(Z lt k) .1271
• (b) P(Z lt k) .9495
• (c) P(Z gt k) .8186
• (d) P(Z gt k) .0073
• (e) P( 0.90 lt Z lt k) .1806
• (f) P( k lt Z lt 1.02) .1464

16
Normal Distribution

• Any normal random variable, X, can be converted
  to a standard normal random variable
• z (x µx)/sx

17
Normal Distribution

• Given a random Variable X having a normal
  distribution with µx 10 and sx 2, find the
  probability that X lt 8.

z
x
4
6
8
10
12
14
16
18
Normal Distribution

• EX The engineer responsible for a line that
  produces ball bearings knows that the diameter of
  the ball bearings follows a normal distribution
  with a mean of 10 mm and a standard deviation of
  0.5 mm. If an assembly using the ball bearings,
  requires ball bearings 10 1 mm, what percentage
  of the ball bearings can the engineer expect to
  be able to use?

19
Normal Distribution

• EX Same line of ball bearings.
• What is the probability that a randomly chosen
  ball bearing will have a diameter less than 9.75
  mm?
• What percent of ball bearings can be expected to
  have a diameter greater than 9.75 mm?
• What is the expected diameter for the ball
  bearings?

20
Normal Distribution

• EX If a certain light bulb has a life that is
  normally distributed with a mean of 1000 hours
  and a standard deviation of 50 hours, what
  lifetime should be placed in a guarantee so that
  we can expect only 5 of the light bulbs to be
  subject to claim?

21
Normal Distribution

• EX A filling machine produces 16oz bottles of
  Pepsi whose fill are normally distributed with a
  standard deviation of 0.25 oz. At what nominal
  (mean) fill should the machine be set so that no
  more than 5 of the bottles produced have a fill
  less than 15.50 oz?

22
Relationship between the Normal and Binomial
Distributions

• The normal distribution is often a good
  approximation to a discrete distribution when the
  discrete distribution takes on a symmetric bell
  shape.
• Some distributions converge to the normal as
  their parameters approach certain limits.
• Theorem 6.2 If X is a binomial random variable
  with mean µ np and variance s2 npq, then the
  limiting form of the distribution of Z (X
  np)/(npq).5 as n ? ?, is the standard normal
  distribution, n(z0,1).

23
Relationship between the Normal and Binomial
Distributions

• Consider b(x15,0.4). Bars are calculated from
  binomial. Curve is normal approximation to
  binomial.

24
Relationship between the Normal and Binomial
Distributions

• Let X be a binomial random variable with n15 and
  p0.4.
• P(X5) ?
• Using normal approximation to binomial
• n(3.5ltxlt4.5µ6, s1.897) ?
• Note, µ np (15)(0.4) 6
• s (npq).5 ((15)(0.4)(0.6)).5 1.897

25
Relationship between the Normal and Binomial
Distributions

• EX Suppose 45 of all drivers in a certain state
  regularly wear seat belts. A random sample of 100
  drivers is selected. What is the probability
  that at least 65 of the drivers in the sample
  regularly wear a seatbelt?