Pre-processing

1
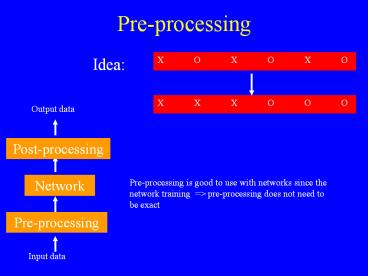
Pre-processing

• Idea

X O X O X O
X X X O O O
Output data
Post-processing
Network
Pre-processing is good to use with networks since
the network training gt pre-processing does not
need to be exact
Pre-processing
Input data
2

• Why Pre-process?
• Although in principle networks can approximate
  any function in practice its easier if
  pre-processing is performed first
• Types of pre-processing
• 1. Linear transformations
• e.g input normalisation
• 2. Dimensionality reduction
• loss of info. Good pre-proc gt lose irrelevant
  info and retain salient features
• 3. Incorporate prior knowledge
• look for edges / translational invariants

3

• 4. Feature extraction
• use a combination of input variables can
  incorporate 1, 2 and 3
• 5. Feature selection
• decide which features to use

4
e.g. Character recognition
b
For a 256 x 256 character we have 65, 536
pixels. One input for each pixel is bad for many
reasons

• Poor generalisation data set would have to be
  vast to be able to properly constrain all the
  parameters (Curse of Dimensionality)
• Takes forever to train
• Answer use e.g. averages of N2 pixels
  dimensionality reduction each average could be
  a feature.
• Which ones to use (select)? Use prior knowledge
  of where salient bits are for different letters

5
Be careful not to over-specify e.g if X was in
one of k classes could use the posterior
probabilities P(Ck X) as features. Therefore,
in principle only k-1 features are needed. In
practice, its hard to obtain P(Ck X) and so we
would use a much larger number of features to
ensure we dont throw out the wrong thing Notice
that the distinction between network training and
pre-proc. is artificial If we got all the
posterior probs. the classification is complete.
Leave some work for the network to do.
6
Input normalisation
Useful for RBFNs (and MLPs) if variation in one
parameter is small with respect to the others it
will contribute very little to distance measures
(l e)2 l2. Therefore, preprocess data to give
zero mean and unit variance via simple
transformation x (x - m) s
7
However, this does not take into account
correlations in the data.
Can be better to use whitening (Bishop, 1995, pp
299-300)
8
Eigenvectors and eigenvalues If Ax lx
For some scalar l not to 0, then we say that x
is an eigenvector with eigenvalue l. Clearly, x
is not unique e.g. if Ax lx, A2x l2x, so it
is usual to scale x so that it has unit
length. Intuition direction of x is unchanged
by being transformed by A so it in some sense
reflects the principal axis of the
transformation.
9
Eigenvector Facts If the data is D-dimensional
there will be D eigenvectors If A is symmetric
(true if A is the covariance matrix), the
eigenvectors will be orthogonal and unit length
so xiT xj 1 if i j xiT xj 0
else This means that the eigenvectors form a set
of basis vectors. That is, any vector can be
expressed as a linear sum of the eigenvectors.
10
Let U be a matrix whose columns are the
eigenvectors ui of A, and L a matrix with the
corresponding eigenvalues li on the diagonals
i.e U (u1, , un) And L diag(l1,
, ln) So AU UL Because of orthogonality of
the eigenvectors U is orthonormal I.e UT U
U-1 U I (that is diag(1, , 1)) Thus we
have the orthogonal similarity transformation UT
AU UT U L L By which we can transform A
into a diagonal matrix
11
Also if A is the covariance matrix of
multivariate normal data, eigenvectors/eigenvalues
reflect the direction and extent of variation ie
Standard deviation in each direction eigenvalue
12
If A is diagonal, eigenvectors are oriented along
the axes If A is the identity, A is circular
13
Whitening
x L-1/2 UT (x - m) where U is a matrix
whose columns are the eigenvectors ui of S, the
covariance matrix of the data, and L a matrix
with the corresponding eigenvalues li on the
diagonals and m is the mean of the data Why?
Because the new covariance matrix will be
approximately the identity matrix
14

• Dimensionality Reduction
• Clearly losing some information but this can be
  helpful due to curse of dimensionality
• Need some way of deciding what dimensions to keep
• Random choice
• Principal components analysis (PCA)
• Independent components analysis (ICA)
• Self-organised maps (SOM)
• etc

15

• Random subset selection
• Any suitable algorithm can be used especially
  ones used in selecting number of hidden units
• Sequential forward search
• Sequential backward search
• Plus-l take away r
• etc

16
Principle Components Analysis Transform the data
into a lower dimensional space but lose as little
information as possible Project the data onto
unit vectors to reduce the dimensionality of the
data. What vectors to use?
x
y y 1
x xT y yT x
17
Want to reduce the dimensionality of x from d to M
x
x
x
x
x
x
x
x
18
Therefore to minimise E we discard the dimensions
with the smallest eigenvectors
19
PCA can also be motivated from considerations of
the variance along an axis specified by the
eigenvectors
20

• PCA procedure
• Given a data set X x1, , xN normalise the
  data (minus mean and divide by the std deviation)
  and calculate the covariance matrix C
• Calculate the eigenvalues li and eigenvectors ui
  of C and order them from 1 to d in decending
  order starting with the largest eigenvalue
• Discard the last d-M dimensions and transform the
  data via

Ie zi are the principal components (NB some books
refer to the ui as the principal components)
21
Why use input normalisation? Must subtract the
mean vector as the theory requires that the data
are centred at the origin Also, we divide by the
standard deviation as we must do something to
ensure that input dimensions with a large range
do not dominate the variance terms Why not use
whitening? Since this removes the correlations
that we are trying to find and makes all the
eigenvalues similar
22
Should result in losing unnecessary information
Here the data is best viewed along the dimension
of the eigenvector with the most variance as this
shows the 2 clusters clearly
23
But it is not guaranteed to work
Here projecting the data onto u1, the eigenvector
with the most variance, loses all discriminatory
information
24
Finally How to decide M ie how many/which
dimensions to leave out? This may be decided in
advance due to constraints on processing
power Another technique (used in eg Matlab) is to
look at the contribution to the overall variance
of each principal component and leave out any
dimensions which fall below a certain
threshold As ever, no one answer may just want
to try a few combinations or could even keep them
all
25

• PCA is very powerful in practical applications.
  But how do we compute eigenvectors and thus
  principal components in real situations?
• Basically two ways Batch and sequential
• We have seen the batch method, but this can be
  impractical if the dimensionality or no. of data
  points is too large
• Also in a nonstationary environment, sequential
  can track gradual changes in the data
• It requires less storage space
• Sequential mode is used in modelling
  self-organization
• It mimics Hebbian learning rule

26
Hebbian Learning
Hebb's postulate of learning (or simply Hebb's
rule) (1949), is the following "When an axon of
cell A is near enough to excite cell B and
repeatedly or persistently takes part in firing
it, some growth processes or metabolic changes
take place in one or both cells such that A's
efficiency as one of the cells firing B, is
increased".
then
Ie if
However, simple hebbian learning cause
uncontrolled growth of weights to a max value so
need to impose a normalisation constraint
Where a is a ve constant known as Ojas rule
(1982) which makes w2 gradually relax to 1/ a
form of competition between synapses
27
In this way networks can exhibit selective
amplification if there is one dominant
eigenvector (cf PCA) How can such precise tuning
come about? Hebbian learning
28
Relationship between PCA and Hebbian
learning Consider a single neuron with a Hebbian
learning rule
w1(t)
input x(t)
output y(t) wT(t) x(t)
wd(t)
Ojas learning rule (Oja, 1982) wi(t1)
wi(t) h y(t) (xi(t) y 2(t) wi (t)) Where
y(t) xi (t) is the Hebbian term and y2(t) wi
(t) is the normalisation term which avoids
uncontrolled growth of the weights (gt w 1
at convergence)
29

• This can be shown to have a stable minimum at
• C w l 1 w
• Where C is the the covariance matrix of the
  training data . Result w(t) converges to w the
  eigenvector of C which has the largest eigenvalue
  l 1 .
• The output is therefore
• y wT x u1T x
• Ie the first principal component of C
• Thus a single linear neuron with a Hebbian
  learning rule can evolve into a filter for the
  first principal component
• Intuitively, consider the 1D case here the
  eigenvector w is either 1 or 1. At convergence
  of Ojas learning rule we have
  
• y(t) (x -y(t) w (t))0 which is satisfied if
  w(t)1 or -1

30
We now introduce a special PCA learning rule
called APEX developed by Kung and Diamantaras,
1990. This is a generalisation of the single
neuron case to multiple neurons where the outputs
are connected via inhibitory links
w11(t)
y1(t)
w1d(t)
aj1(t)
input x(t)
y2(t)
ajd(t)
wdd(t)
output j yj(t) wj T(t) x(t) ajT(t) yj-1(t)
Where we define the feedback vector yj-1
y1(t), y2(t) , yj-1(t) Wj(t) wj1(t),
wj2(t) , wjd(t) and aj(t) aj1(t), aj2(t)
, ajd(t)
31
Where the update rules for wj and aj
are wj(t1) wj(t) h yj(t) (x(t) - y2j(t)
wj (t)) (Hebbian normalisation) aj(t
1) aj(t) - h yj(t)(yj-1(t)y2j(t) aj(t))
(anti-Hebbian (inhibitory)
normalisation) Procedure to find the yi (ie the
principal components) is analogous to proof by
induction if we have found (y1 , y1 , yi-1 )
we can determine the feedback vector yi-1(t)
y1(t), ...., yj-1(t)
32
Apex algorithm 1. Initialize the feedforward
weight vector wj and the feedback weight vector
aj to small random values at time t 1, where j
1, 2, , d. Assign a small positive value for
h. 2. Set j1 and compute the first principal
component y1 as for the single neuron ie for t
1, 2, 3, compute y1(t) w1T(t)
x(t) w1(t1) w1(t) h y1(t) (x(t) - y1(t)
w1(t)) (Continued overleaf )
33

• Set j2 and for t 1, 2, 3, compute
• yj-1(t)y1(t), ...., yj-1(t) (the
  feedback)
• yj(t) wj T(t) x(t) ajT(t) yj-1(t)
• wj(t1) wj(t) h yj(t) (x(t) - yj(t) wj
  (t))
• aj(t1) aj(t) - h yj(t)(yj-1(t)yj(t)
  aj(t))
• 4. Increase j by 1 and go to step 3. Repeat
  till j M the desired number of dimensions

34
Theoretically, PCA is the optimal (in terms of
not losing information) way to encode high
dimensional data onto a lower dimensional
subspace Can be used for data compression where
intuition is that getting rid of dimensions with
little variance gets rid of noise
35
Independent Components Analysis (ICA) As the
name implies, an extension of PCA but rooted in
information theory. Starting point suppose we
have the following situation
Observation vector x(n)
Demixer W
Mixer A
Output vector y(n)
Source vector u(n)
Unknown environment
36
That is we have a number of vectors of values
(indexed by n eg data at various time-steps)
generated by d independent sources u(n) (u1
(n), , ud (n) ) (assumed to have zero mean)
which have been mixed by a d x d matrix A to give
a vector of observations x(n) (x1 (n), , xd
(n) ) (also zero mean as u zero mean). That is
x (n) A u (n) Where A
and u(n) are unknown. The problem is to recover u
when all we know (all we can see) are the
observation vectors x Problem therefore known as
blind source separation
37
Example u1 (t) 0.1 sin (400 t )cos( 30
t) u2 (t) 0.001 sign (sin(500 t 9cos (40
t))) u3 (t) uniformally distributed noise
in the range -1,1
x1 (t) 0.56 u1 (t) 0.79 u2 (t) -0.37 u3 (t)
x2 (t) -0.75 u1 (t) 0.65 u2 (t) 0.86 u3 (t)
x3 (t) 0.17 u1 (t) 0.32 u2 (t) -0.48 u3
(t) Problem we receive signals x(t), how do we
recover u(t)?
38
u1(t)
u2(t)
u3(t)
39
x1(t)
x2(t)
x3(t)
40
To solve this we need to find a matrix W such
that y(n) W x(n) with the property that
u can be recovered from the outputs y. Thus the
blind source separation problem can be stated
as
Given N independent realisations of the
observation vector x, find an estimate for the
inverse of the mixing matrix A
since y(n) W x(n) A-1 x(n) A-1 A u(n)
u(n)
41
Neurobiological correlate the cocktail party
problem The brain has the ability to to
selectively tune to and follow one of a number of
(independent) voices despite noise, delays, water
in your ear lecturer droning on etc etc Very
many applications including Speech analysis for
eg teleconferencing Financial analysis extract
the underlying set of dominant components Medical
sensor interpretation eg separate a foetuses
heartbeat from the mothers (Sussex) neuroscience
(Ossorio, Baddeley and Anderson) analysis of
cuttlefish patterns. Try to find an underlying
alphabet/language of patterns used to convey
information
42
Use Independent Component Analysis (Comon, 1994)
Can be viewed as an extension of PCA as both aim
to find linear sums of components to re-represent
the data In ICA, however, we impose statistical
independence on the vectors found and lose the
orthogonality constraint Definition random
variables X and Y are statistically independent
if joint probability density function can be
expressed as a product of the marginal density
functions (ie pdfs of X and Y as if they were on
their own) f(x, y) f(x) f(y) NB discrete
analogy if A and B are independent events
then P(A and B) P(A, B) P(A) P(B)
43
PCA
ICA
PCA good for gaussian data, ICA good for non
gaussian as indpendence gt non-gaussianity In
fact, independent components MUST be nongaussian
(more interesting distributions if non-gaussian)
and to get components we maximise the
non-gaussianity (the kurtosis) of the data Why?
Because a linear sum of gaussians is itself
gaussian and one cannot distinguish the
components from the mixture model
44
Young field (mid 90s), still developing,
somewhat in concurrence with kernel techniques
(eg kernel PCA and kernel ICA find non-linear
combinations of components to represent the
data) Need some measure of statistical
independence of X and Y Can use mutual
information I(X, Y) Concept from information
theory defined in terms of entropy which is a
measure of the average amount of information a
variable conveys, or analogously our uncertainty
about the variable If X is the system input and
Y the system output, the mutual information I(X,
Y) is the difference in our levels of uncertainty
about the system input (its entropy) before and
after observing the system output. Thus if
I(X, Y) 0 X and Y are statistically
independent or intuitively no information about
X from Y and vice versa gt X, Y independent
45
Idea, therefore is to minimise the mutual info
I(yi,, yj) between all pairs I and j of the
outputs (which we want to be equal to the
original inputs which are independent) This is
equivalent to minimising the Kullback-Leibler
(KL) divergence which measures the difference
between the joint pdf f(y,W) and the product of
the marginal densities f(yi,W) with respect to
W. Thus we have (a variant of) the Infomax
Principle (Comon) Given a d-by-1 vector x
representing a linear combination of d
independent source signals, the transformation of
the observation vector x by a neural system into
a new vector y should be carried out in a way
that the KL divergence between the paramaterised
probability density function f(y,W) and the
product of the marginal densities f(yi,W) is
minimised with respect to the unknown parameter
matrix W
46

• Which after some hard maths (Haykin 10.11 and
  other bits of chapter 10) leads us to the
  following algorithm for finding W
• W(n 1) - W(n) h( n) I - f (y(n))yT(n) W(n)
• where
• (y) f (y1), f (y2) , , f (ym)T
• And

NB h must be chosen to be sufficiently small for
stability of the algorithm (see Haykin). Many
other versions are available (FastICA seems quite
good) Return to the problem described earlier
47
u1 (t) 0.1 sin (400 t )cos( 30 t) u2
(t) 0.001 sign (sin(500 t 9cos (40 t)))
u3 (t) uniformally distributed noise in the
range -1,1
x1 (t) 0.56 u1 (t) 0.79 u2 (t) -0.37 u3 (t)
x2 (t) -0.75 u1 (t) 0.65 u2 (t) 0.86 u3 (t)
x3 (t) 0.17 u1 (t) 0.32 u2 (t) -0.48 u3
(t) Problem we receive signals x(t), how do we
recover u(t)?
48
u1(t)
u2(t)
u3(t)
49
x1(t)
x2(t)
x3(t)
50
Using the blind separation learning rule starting
from random weights in the range 0, 0.05, h
0.1, N65000, timestep 1x 10-4, batch version
of algorithm for stability (Haykin, p.544)
0.0109 0.0340 0.0260 W(0)
0.0024 0.0467 0.0415 0.0339
0.0192 0.0017
0.2222 0.0294 -0.6213 W(t) converges to
-10.1932 -9.8131 -9.7259 around
t300 4.1191
-1.7879 -6.3765
2.5 0 0 where WA
0 17.5 0
0 0 0.24 W is almost an inverse of A
(with scaling of the original signals as the
solution not unique) and so the signal is
recovered
51
Components can only be estimated up to a
rescaling (since if x is a component multiplied
by a, then 2x multiplied by a/2 is also a
component Note that this means we often get x
instead of x
52
Pre-processing in ICA
Must pre-process before performing ICA to give
the data zero mean Also helps to whiten the data
as it makes the mixing matrix orthogonal which
means there are less parameters to estimate
(since AT A) Often good to reduce the
dimensionality (via PCA etc) to get rid/reduce
noise
53
ICA example 2 Original Sources
54
ICA Example 2 Mixed images
55
ICA Example 2 PCA/whitened images
56
ICA Example 2 Extracted components
57
ICA Example 2 rescaling of ve components
58
Example 1 Speech - Music Separation A speaker
has been recorded with two distance talking
microphones (sampling rate 16kHz) in a normal
office room with loud music in the background.
The distance between the speaker, cassette player
and the microphones is about 60cm in a square
ordering.
Microphone 1
Microphone 2
Separated source 1
Separated source 2
59
2. Speech - Speech Separation A real Cocktail
Party Effect . Two Speakers have been recorded
speaking simultaneously. Speaker 1 says the
digits from one to ten in English and speaker 2
counts at at the same time the digits in Spanish
(uno dos ... ) The recording has been done in a
normal office room. The distance between the
speakers and the microphones is about 60cm in a
square ordering
Microphone 1
Microphone 2
Separated source 1
Separated source 2
60
3. Speech - Speech Separation in difficult
environments A real Cocktail Party Effect II .
Two Speakers have been recorded speaking
simultaneously. This time the recording was in a
conference room ( 5.5m by 8m ). The conference
room had some air-conditioning noise. Both
speakers are reading a section from the newspaper
for 16sec. The mics were placed 120 cm away from
the speakers. The unmixing filters need to be
sufficiently long. We used a filter size of 2048
taps for each filter.
Microphone 1
Microphone 2
Separated source 1
Separated source 2
61
Pre-processing for time series
Problem prediction of time series data ie
sequence of measurements taken at regular time
intervals. e.g. share price, weather forecast,
speech signals etc Take 1D case for simplicity,
x(t) network attempts to approximate the x(t)
from the previous d outputs x(t - d), , x(t
1) used as inputs one-step ahead
prediction Could try to predict more steps ahead
(multi-step ahead prdeiction) but the errors tend
to accumulate quickly and such efforts are
usually characterised by a sharp decrease in
performance
62
Here we are attempting to fit the static function
which is underlying the fluctuations That is, if
there is a general trend (eg increase with time)
we want to remove it de-trending That is, we
first attempt to fit a simple (eg linear)
function of time to the data and then take this
away from the inputs However, if the trend
itself evolves with time this is inappropriate
and on-line techniques are needed to track the
data. How to do this well is an open research
issue
63
Prior knowledge can also be used to improve
network training and performance
Several ways of incorporating prior knowledge eg
invariances 1. If we know the network is
invariant to some transformations of the data we
could pre-process the data set X by forming
invariants of members of the data set and adding
them to a new data set X however, this can
quickly lead to very large data sets 2. Simply
remove invariant points by pre-processing If
we are classifying lists of properties and the
order is unimportant, pre-process the data so
that the lists are all mapped to a unique
ordering, eg alphabetical