Chapter 14: Elements of Nonparametric Statistics

1
Chapter 14 Elements of Nonparametric Statistics
2
Chapter Goals

• Introduce the basic concepts of nonparametric
  statistics, or distribution-free techniques.
• Nonparametric statistics are versatile and easy
  to use.
• Consider some of the most common tests and
  applications.

3
14.1 Nonparametric Statistics

• Parametric methods Assume the population is at
  least approximately normal, or use the central
  limit theorem.
• Nonparametric methods, or distribution-free
  methods Assume very little about the population,
  subject to less confining restrictions.

4

• Nonparametric statistics have become popular
• 1. Require few assumptions about the underlying
  population.
• 2. Generally easier to apply than their
  parametric counterparts.
• 3. Relatively easy to understand.
• 4. Can be used in situations where the normality
  assumptions cannot be made.
• 5. Generally only slightly less efficient than
  their parametric counterparts.
• Disadvantages?

5
14.2 Comparing Statistical Tests

• Four nonparametric tests presented in this
  chapter. There are many others.
• Many nonparametric tests may be used as well as
  certain parametric tests.
• Which statistical test is appropriate the
  parametric or nonparametric.

6

• Which test is best?
• 1. When comparing two tests they must be equally
  qualified for use they must both be appropriate
  test procedures.
• 2. Each test has a set of assumptions that must
  be satisfied.
• 3. The best test The test that is best able to
  control the risks of error and at the same time
  keeps the sample size reasonable.
• 4. A larger sample size usually means a higher
  cost.

7

• The Risk of Error
• 1. Type I Error Controlled directly (set) by the
  level of significance a.
• 2. P(type I error) a, P(type II error) b
• 3. We try to control b.
• 4. The power of a statistical test 1 - b
• The power of a test is the probability that we
  reject the null hypothesis when it is false (a
  correct decision).
• If two appropriate statistical tests have the
  same significance level a, the one with the
  greater power is better.

8

• The sample size
• 1. Set acceptable values for a and b. Determine
  the sample size necessary to satisfy these
  values.
• 2. The statistical test that requires the smaller
  sample size is better.
• 3. Efficiency The ratio of the sample size of
  the best parametric test to the sample size of
  the best nonparametric test when compared under a
  fixed set of risk values.
• Example Efficiency rating for the sign test is
  approximately 0.63. This means that a sample of
  size 63 with a parametric test will do the same
  job as a sample of size 100 for the sign test.

9

• To determine the choice of test
• 1. Often forced to use a certain test because of
  the nature of the data.
• 2. When there is a choice, consider three
  factors
• a. The power of the test.
• b. The efficiency of the test.
• c. The data (and the sample size).
• Note The following table shows a comparison of
  nonparametric tests (presented in this chapter)
  with the parametric tests presented earlier.

10

• Comparison of Parametric and Nonparametric Tests

11
14.3 The Sign Test

• Versatile, easy to apply, uses only plus and
  minus signs.
• Three sign test applications confidence interval
  for a median, hypothesis test concerning a
  median, hypothesis test concerning the median
  difference (paired difference) for two dependent
  samples.

12

• Assumptions for inferences about the population
  median using the sign test The n random
  observations forming the sample are selected
  independently and the population is continuous in
  the vicinity of the median, M.
• Procedure for using the sign test to obtain a
  confidence interval for an unknown population
  median, M
• 1. Arrange the data in ascending order (smallest
  to largest)
• x1 (smallest), x2, x3, . . . , xn (largest)
• 2. Use Table 12, Appendix B to obtain the
  critical value, k (the maximum allowable number
  of signs).
• 3. k indicates the number of positions to be
  dropped from each end of the ordered data.
• 4. The remaining extreme values are the bounds
  for a 1 - a confidence interval.
• Confidence Interval xk1 to xn-k
• Note Based on the binomial distribution.

13

• Example Suppose 20 observations are selected at
  random and are given in ascending order (x1, x2,
  x3, . . . , x20).
• 19 21 23 28 31 32 33 34
  34 35
• 38 41 43 43 44 46 47 48
  52 55
• Find a 95 confidence interval for the population
  median.
• Solution
• Table 12 n 20, a 0.05 Þ k 5
• Drop the last 5 values on each end.
• The confidence interval is bounded by x6 and x10.
• The confidence interval 32 to 44 (inclusive).
• In general xk1 to xn-k is a 1 - a confidence
  interval for M.

14

• Single-Sample Hypothesis Test Procedure
• 1. The sign test may be used when the null
  hypothesis concerns the population median M.
• 2. The test may be either one- or two-tailed.
• Example A random sample of 88 tax payers was
  selected and each was asked the amount of time
  spent preparing their federal income tax return.
  Test the hypothesis the median time required to
  prepare a return is 8 hours against the
  alternative that the median is greater than 8
  hours.
• The data is summarized by
• Under 8 37 Equal 8 3 Over 8 48
• Use the sign test with a 0.025.

15

• Solution
• The data is converted to () and (-) signs
  according to whether the data is more or less
  than 8.
• A plus sign is assigned to each observation
  greater than 8.
• A minus sign is assigned to each observation less
  than 8.
• A zero is assigned to each observation equal to
  8.
• The sign test uses only the plus and minus signs.
• The zeros are discarded.
• Usable sample size 88 - 3 85
• n() 48 n(-) 37
• n() n(-) n 85

16

• 1. The Set-up
• a. Population parameter of concern M,
  population median time to prepare a federal
  income tax return.
• b. The null and alternative hypothesis
• H0 M 8
• Ha M gt 8
• 2. The Hypothesis Test Criteria
• a. Assumptions The 88 observations were
  randomly selected and the variable time to
  prepare a return is continuous.
• b. Test statistic x the number of the less
  frequent sign n(-)
• c. Level of significance a 0.025

17

• 3. The Sample Evidence
• n 85 x n(-) 37
• 4. The Probability Distribution (Classical
  Approach)
• a. Critical value The critical region is
  one-tail.
• Table 12 is for two-tailed tests.
• At the intersection of the column a 0.05 ( 2
  0.025) and the row n 85 k 32.
• The critical value k 32.
• b. x is not is the critical region.

18

• 4. The Probability distribution (p-Value
  Approach)
• a. The p-value Using Table 12 P gt (0.25/2)
  0.125
• Using a computer P 0.1928
• b. The p-value is larger than the level of
  significance, a.
• 5. The Results
• a. Decision Do not reject H0.
• b. Conclusion At the 0.025 level of
  significance, there is no evidence to suggest
  the median time required to complete a federal
  income tax return is greater than 8 hours.

19

• Two Sample Hypothesis Test Procedure
• 1. The sign test may also be used in tests
  concerning the median difference between paired
  data that result from two dependent samples.
• 2. A common application the use of
  before-and-after testing to determine the
  effectiveness of some activity.
• 3. The signs of the differences are used to carry
  out the test. Zeros are discarded.
• Assumptions for inferences about median of paired
  differences using sign testThe paired data is
  selected independently and the variables are
  ordinal or numerical.

20

• Example A new automobile engine additive
  (included during an oil change) is designed to
  decrease wear and improve engine performance by
  increasing gas mileage. Sixteen randomly selected
  automobiles were selected and the
  before-and-after miles per gallon were recorded.
  (The same driver was used before and after the
  engine treatment.) Is there any evidence to
  suggest the engine additive improves gas mileage?
  Use a 0.05.
• Note The claim being tested is that the additive
  improves gas mileage. Form all the differences,
  After - Before. We will only reject the null
  hypothesis if there are significantly more plus
  signs.

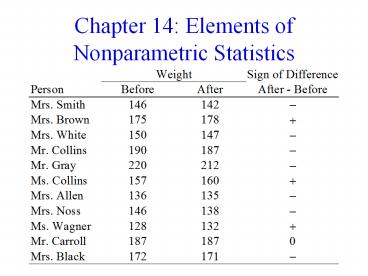
21

• Data

22

• 1. The Set-up
• a. Population parameter of concern
• M, median gain in miles per gallon.
• b. The null and alternative hypothesis
• H0 M 0 (no mileage gain)
• Ha M gt 0 (mileage gain)
• 2. The Hypothesis Test Criteria
• a. Assumptions The automobiles were randomly
  selected and the variables, miles per gallon
  before and after, are both continuous.
• b. Test statistic The number of the less
  frequent sign.
• In this example x n(-)
• c. Level of significance 0.05

23

• 3. The Sample Evidence
• n 16 n() 10 n(-) 6
• Observed value of the test statistic x n(-)
  6
• 4. The Probability Distribution (Classical
  Approach)
• a. Critical Value The critical region is
  one-tail.
• Table 12 is for two-tailed tests.
• At the intersection of the column a 0.10 ( 2
  0.05) and the row n 16 k 4.
• The critical value k 4.
• b. x is not in the critical region.

24

• 4. The Probability Distribution (p-Value
  Approach)
• a. The p-value Using Table 12 P gt (0.25/2)
  0.125
• Using a computer P 0.2272
• b. The p-value is larger than the level of
  significance, a.
• 5. The Results
• a. Decision Do not reject H0.
• b. Conclusion At the 0.05 level of
  significance, there is no evidence to suggest
  the engine additive increases the miles per
  gallon.

25

• Normal Approximation
• 1. The sign test may be carried our using a
  normal approximation and the standard normal
  variable z.
• 2. The normal approximation is used if Table 12
  does not show the desired level of significance
  or if n is large.
• Procedure
• 1. x is the number of the less frequent sign or
  the most frequent sign consistent with the
  alternative hypothesis.
• 2. x is a binomial random variable with p 0.5.

26

• 3. x is a binomial random variable, but it does
  become approximately normal for large n.
• Problem A binomial random variable is discrete
  and a normal random variable is continuous.
• Solution Use the continuity correction an
  adjustment in the normal random variable so that
  the approximation is more accurate.
• Continuity Correction
• a. For the binomial random variable, the area of
  a rectangular bar represents probability
  width 1, from 1/2 unit below to 1/2 unit above
  the value of interest.
• b. When z is used, make a 1/2 unit adjustment
  before calculating the observed value of z.
• c. x is the adjusted value for x.
• If x gt n/2 then x x - (1/2)
• If x lt n/2 then x x (1/2)

27

• Continuity Correction Illustration

P(x 7) P(6.5 x 7.5)
discrete
continuous
28

• 1 - a confidence interval for M
• Using the normal approximation (including the
  continuity correction), the position numbers are
• The interval is xL to xU where
• Note L should be rounded down and U should be
  rounded up to be sure the level of confidence is
  at least 1 - a.

29

• Example Estimate the population median with a
  95 confidence interval for a given data set with
  55 observations x1, x2, x3, . . . , x54, x55.
• Solution
• The position numbers are
• L 27.5 - 7.77 19.73 rounded down, L 19.
• U 27.5 7.77 35.27 rounded up, U 36.
• Therefore 95 confidence interval for M x19 to
  x36.

30

• Hypothesis test concerning M
• Using the standard normal distribution, z is
  computed using the formula
• Example In a recent study children between the
  ages of 8 and 12 were reported to watch a median
  of 18 hours of television per week. In order to
  test this claim, 105 children between 8 and 12
  were selected at random and the number of hours
  of television watched per week were recorded. A
  plus sign was coded if the number of hours was
  greater than 18, a minus sign if less than or
  equal to18 there were 71 plus signs and 34 minus
  signs. Use the normal approximation to the sign
  test to determine if there is any evidence to
  suggest the median number of hours watched is
  greater than 18. Use a 0.05

31

• Solution
• 1. The Set-up
• a. Population parameter of concern M, the
  median number of hours of television watched
  per week.
• b. The null and alternative hypothesis
• H0 M 18 () (at least as may minus signs as
  plus signs)
• Ha M gt 18 (fewer minus signs than plus signs)
• 2. The Hypothesis Test Criteria
• a. Assumptions The random sample of 105
  students was independently surveyed and the
  variable, hours of television watched per week,
  is continuous.
• b. Test statistic z
• c. Level of significance a 0.05

32

• 3. The Sample Evidence
• a. Sample information n() 71, n(-) 34
• n 105 and x 71
• b. Calculate the value of the test statistic
• 4. The Probability Distribution (Classical
  Approach)
• a. Critical value z(0.05) 1.65
• b. z is in the critical region.

33

• 4. The Probability Distribution (p-Value
  Approach)
• a. The p-value P P(z gt 3.51) 0.0002
• Using a computer P 0.000224
• b. The p-value is smaller than the level of
  significance, a.
• 5. The Results
• a. Decision Reject H0.
• b. Conclusion At the 0.05 level of
  significance, there is evidence to suggest the
  median number of hours of television watched
  per week is greater than 18.

34
14.4 The Mann-Whitney U Test

• Nonparametric alternative for the t test for the
  difference between two independent means.
• Null hypothesis the two sampled populations are
  identical.

35

• Assumptions for inferences about two populations
  using the Mann-Whitney test
• The two independent random samples are
  independent within each sample as well as between
  samples, and the random variables are ordinal or
  numerical.
• Note
• 1. This test procedure is often applied in
  situations in which the two samples are drawn
  from the same population of subjects, but
  different treatments are used on each sample.
• 2. Test procedure described in the following
  example.

36

• Example A recent study claimed that adults who
  exercise regularly tend to have lower pulse
  rates. To test this claim, two independent random
  samples of adult males were selected, one from
  those who exercise regularly (A), and one from
  those who are more sedentary (B). The data is
  given below. Is there any evidence to suggest
  that adults who exercise regularly have lower
  pulse rates than those who do not exercise
  regularly. Use a 0.05.

37

• Solution
• 1. The Set-up
• a. Population parameter of concern The
  distribution of pulse rates for each
  population of adult males.
• b. The null and alternative hypothesis
• H0 Populations A and B have pulse rates with
  identical distributions.
• Ha The two distributions are not the same.
• 2. The Hypothesis Test Criteria
• a. Assumptions The two samples are independent,
  and the random variable (pulse rate) is
  numerical.
• b. Test statistic Mann-Whitney U Statistic,
  described below.
• c. Level of significance a 0.05

38

• 3. The Sample Evidence
• a. Sample information Data given in the table
  above.
• b. Calculate the value of the test statistic
• na sample size from population A
• nb sample size from population B
• Combine the two samples and order the data from
  smallest to largest.
• Assign each observation a rank number.
• The smallest observation is assigned rank 1,
  the next smallest is assigned rank 2, etc., up
  to the largest, which is assigned rank na nb.
• For ties assign each of the tied observations
  the mean rank of those rank positions that
  they occupy.

39

• The rankings

40

• To Compute the U Statistic
• 1. Compute the sum of the ranks for each of the
  two samples Ra and Rb.
• 2. Compute the U score for each sample
• 3. The test statistic, U, is the smaller of Ua
  and Ub.

41

• In this example

42

• Background
• 1. Suppose the two samples are very different.
• Small ranks are associated with one sample,
  large ranks with the other.
• U would tend to be small, and we would want to
  reject the null hypothesis.
• 2. Suppose the two samples are very similar.
• The ranks are evenly distributed between the two
  samples.
• Ua and Ub tend to be about equal, U tends to be
  larger.
• Note Ua Ub na nb
• Therefore only need to consider the smaller
  U-value.

43

• 4. The Probability Distribution (Classical
  Approach)
• a. Critical value Use Table 13B, one-tailed, a
  0.05
• Critical value is at the intersection of column
  n1 10 and row n2 10 27
• b. U is not in the critical region.
• 4. The Probability Distribution (p-Value
  Approach)
• a. The p-value P P(U 30, for n1 10 and
  n2 10)
• Using Table 13 P gt 0.05
• Using a computer P 0.0694
• b. The p-value is not smaller than a.

44

• 5. The Results
• a. Decision Do not reject H0.
• b. Conclusion At the 0.05 level of
  significance, there is no evidence to suggest
  the two populations are different.
• Normal Approximation
• If the sample sizes are large, then U is
  approximately normal with
• The standard normal distribution may be used if
  both sample sizes are greater than 10 the test
  statistic is

45

• Example The data below represents the number of
  hours two different cellular phone batteries
  worked before a recharge was necessary. Is there
  any evidence to suggest battery type B lasts
  longer than battery type A. Use the Mann-Whitney
  test with a 0.05.

46

• Solution
• 1. The Set-up
• a. Population parameter of concern The
  distribution of battery life for each brand.
• b. The null and alternative hypothesis
• H0 The distributions for battery life are the
  same for both brands.
• Ha The distributions are not the same.
• 2. The Hypothesis Test Criteria
• a. Assumptions The two samples are independent
  and the random variable, battery life, is
  continuous.
• b. Test statistic Mann-Whitney U statistic
  (normal approximation).
• c. Level of significance a 0.05

47

• 3. The Sample Evidence
• a. Sample information Data given in the table
  above.
• b. Calculate the value of the test statistic
• Rankings for battery life

48

• The sums
• The U scores

49

• Determine the z statistic

50

• 4. The Probability Distribution (Classical
  Approach)
• a. Critical value -z(0.05) -1.65
• b. z is not in the critical region.
• 4. The Probability Distribution (p-Value
  Approach)
• a. The p-value P P(z lt -.6101) .2709
• b. The p-value is not smaller than a.
• 5. The Results
• a. Decision Do not reject H0.
• b. Conclusion At the 0.05 level of
  significance, there is no evidence to suggest
  the battery life for brand B is longer than the
  life for brand A.

51
14.5 The Runs Test

• Used to test the randomness of data (or lack of
  randomness).
• Run a sequence of data with a common property.
• Test statistic, V the number of runs observed.

52

• Example A coin is tossed 15 times and a head (H)
  or a tail (T) is recorded on each toss. The
  sequence of tosses was
• T H T T T H H T T T H H
  T T T
• The number of runs is V 7.
• T H T T T H H T T T H H T T T
• Note
• 1. No randomness only two runs (all heads, then
  all tails, or the other way around). Or H and T
  alternate.
• 2. n1 number of data with property 1.
• n2 number of data with property 2.
• n n1 n2 sample size.

53

• Assumptions for inferences about randomness using
  the Runs test
• Each observation may be classified into one of
  two categories.
• Note
• 1. A large number of runs, or a small number of
  runs, (more or less than what we would expect by
  chance), suggests the data is not random.
• 2. Another aspect of randomness the ordering of
  observations above or below the mean or median
  of the sample.

54

• Example Consider the following sample and use
  the runs test to determine if the sequence is
  random with respect to being above or below the
  mean value.
• Test the null hypothesis that this sequence is
  random.
• Use a 0.05.
• Solution
• 1. The Set-up
• a. Population parameter of concern Randomness
  of the values above or below the mean.

24 27 30 24 29 26 33
27 32 35 25 26 24 25
31 19 15 23 18 20 28
30 25 31 24 23 28 25
26 22 24 15 26 32 17
38
55

• b. The null and the alternative hypothesis
• H0 The numbers in the sample form a random
  sequence with respect to the two properties
  above and below the mean value.
• Ha The sequence is not random.
• 2. The Hypothesis Test Criteria
• a. Assumptions Each observation may be
  classified as above or below the mean.
• b. Test statistic V, the number of observed
  runs.
• c. Level of significance a 0.05

56

• 3. The Sample Evidence
• Compare each number in the original sample to
  the value of the mean to obtain the following
  sequence of as (above) and bs (below).
• b a a b a a a a a a b a
  b b a b b b
• b b a a b a b b a b a b
  b b a a b a
• na 18, nb 18, V 20
• If n1 and n2 are both less than or equal to 20,
  and a two- tailed test with a 0.05 is
  conducted, use Table 14, Appendix B.

57

• 4. The Probability Distribution (Classical
  Approach)
• a. Critical value Two-tailed test, a 0.05,
  Use Table 14.
• Critical values at the intersection of column
  n1 18 and row n2 18 12 and 26.
• b. V is not in the critical region.
• 4. The Probability Distribution (p-Value
  Approach)
• a. The p-value P 2 P(V ³ 20, for na 18
  and nb 18)
• Using Table 14 P gt 0.05
• Using a computer 0.7352
• b. The p-value is not smaller than the level of
  significance, a.

58

• 5. The Results
• a. Decision Do not reject H0.
• b. Conclusion At the 0.05 level of
  significance, there is no evidence to reject
  the null hypothesis that the sequence is random
  with respect to above and below the mean.
• Normal Approximation
• 1. If n1 and n2 are larger than 20, or if a is
  different from 0.05, a normal approximation may
  be used.
• 2. V is approximately normally distributed with
• 3. Test statistic

59

• Example The letters in the following sequence
  represent the direction each car turned after
  exiting at a certain ramp on the New Jersey
  Turnpike (L - left, R - right).
• L L R R R R R R R L L L R R R R L L R R
• R R L L L L L R R L L L R L R L L R R L
• L R R R R R R L L L L L R R R R R R L L
• Test the null hypothesis that the sequence is
  random with regards to direction. Use a 0.01.

60

• Solution
• 1. The Set-up
• a. Population parameter of concern Randomness
  with respect to direction turned after exiting
  the turnpike.
• b. The null and alternative hypothesis
• H0 The sequence of directions (L and R) is
  random.
• Ha The sequence is not random.
• 2. The hypothesis Test Criteria
• a. Assumptions Each observation may be
  classified an L or R.
• b. Test statistic V, the number of runs.
• c. Level of significance a 0.01

61

• 3. The Sample Evidence
• Calculate the value of the test statistic
• From the table above nL 27, nR 33,
  V 19
• Determine the z statistic

62

• 4. The Probability Distribution (Classical
  Approach)
• a. Critical values -z(0.005) -2.58 and
  z(0.005) 2.58
• b. z is in the critical region.
• 4. The Probability Distribution (p-Value
  Approach)
• a. The p-value P 2 P(z lt -3.078) 0.0021
• b. The p-value is smaller that the level of
  significance, a.
• 5. The Results
• a. Decision Reject H0.
• b. Conclusion At the 0.01 level of
  significance, there is evidence to suggest the
  turning direction for cars exiting the turnpike
  is not random.

63
14.6 Rank Correlation

• Charles Spearman developed the rank correlation
  coefficient.
• A nonparametric alternative to the linear
  correlation coefficient (Pearsons product
  moment, r).

64

• Spearman rank correlation coefficient
• di the difference in the paired rankings.
• n the number of pairs.
• Note
• 1. rS will range from -1 to 1.
• 2. rS used in a the same way as the linear
  correlation coefficient r.

65

• Calculation of rS
• 1. Rank the x-values from smallest to largest 1,
  2, ... , n.
• 2. Rank the y-values from smallest to largest 1,
  2, ... , n.
• 3. Use the ranks instead of the actual numerical
  values in the formula for r, the linear
  correlation coefficient.
• 4. If there are no ties, rS is equivalent to r.
• 5. rS is an easier procedure that uses the
  differences between the ranks di.
• 6. In practice, rS is used even when there are
  ties.
• 7. For ties assign each of the tied observations
  the mean rank of those rank positions that they
  occupy.

66

• Assumptions for inferences about rank
  correlation
• The n ordered pairs of data form a random sample
  and the variables are ordinal or numerical.
• Null Hypothesis
• There is no correlation between the two
  rankings.
• Alternative Hypothesis
• Two-tailed There is correlation between
  rankings.
• May be one-tailed if positive or negative
  correlation is suspected.
• Critical Region
• On the side(s) corresponding to the specific
  alternative.
• Table 15, Appendix B positive critical values
  only, add a plus or minus sign to the value
  found in the table, as appropriate.

67

• Example A researcher believes a certain toxic
  chemical accumulates in body tissues with age and
  may eventually cause heart disease. Twelve
  subjects were selected at random. Their age and
  the chemical concentration (in parts per million)
  in tissue samples is given in the table below.
  Is there any evidence to suggest the chemical
  concentration in tissue samples increases with
  age? Use a 0.01.

68

• Solution
• 1. The Set-up
• a. Population parameter of concern Rank
  correlation coefficient between age and
  chemical concentration, rS.
• b. The null and alternative hypothesis
• H0 Age and chemical concentration are not
  related.
• Ha Older people tend to have higher chemical
  concentrations in their tissues.
• 2. The Hypothesis Test Criteria
• a. Assumptions The 12 ordered pairs of data
  form a random sample both variables are
  continuous.
• b. Test statistic Rank correlation coefficient,
  rS.
• c. Level of significance a 0.01.

69

• 3. The Sample Evidence
• The ranks and differences

70

• Use the formula for rS
• 4. The Probability Distribution (Classical
  Approach)
• a. Critical value The critical region is
  one-tailed.
• Table 15 lists critical values for two-tailed
  tests.
• The critical value is located at the
  intersection of the a 0.02 column (2 0.01)
  and the n 12 row 0.703
• b. rS is in the critical region.

71

• 4. The Probability Distribution (p-Value
  Approach)
• a. The p-value P P(rS ³ 0.7535, for n 12)
• Using Table 15 P lt 0.005
• Using a computer P 0.0025
• b. The p-value is smaller than the level of
  significance, a.
• 5. The Results
• a. Decision Reject H0.
• b. Conclusion At the a 0.01 level of
  significance, there is evidence to suggest that
  older people tend to have higher levels of
  chemical concentration in their tissues.

72

• Normal Approximation
• 1. As n gets large, rS approaches a normal
  distribution.
• 2. When n exceeds the values in Table 15, the
  following test statistic may be used