Circuit analysis summary

1
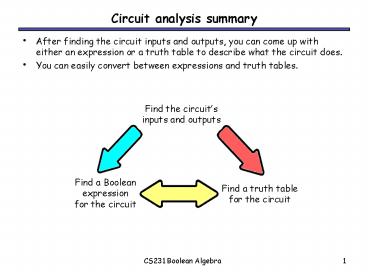
Circuit analysis summary

• After finding the circuit inputs and outputs, you
  can come up with either an expression or a truth
  table to describe what the circuit does.
• You can easily convert between expressions and
  truth tables.

Find the circuits inputs and outputs
Find a Boolean expression for the circuit
Find a truth table for the circuit
2
Boolean operations summary

• We can interpret high or low voltage as
  representing true or false.
• A variable whose value can be either 1 or 0 is
  called a Boolean variable.
• AND, OR, and NOT are the basic Boolean
  operations.
• We can express Boolean functions with either an
  expression or a truth table.
• Every Boolean expression can be converted to a
  circuit.
• Next time, well look at how Boolean algebra can
  help simplify expressions, which in turn will
  lead to simpler circuits.

3
Expression simplification

• Normal mathematical expressions can be simplified
  using the laws of algebra
• For binary systems, we can use Boolean algebra,
  which is superficially similar to regular algebra
• There are many differences, due to
• having only two values (0 and 1) to work with
• having a complement operation
• the OR operation is not the same as addition

4
Formal definition of Boolean algebra

• A Boolean algebra requires
• A set of elements B, which needs at least two
  elements (0 and 1)
• Two binary (two-argument) operations OR and AND
• A unary (one-argument) operation NOT
• The axioms below must always be true (textbook,
  p. 33)
• The magenta axioms deal with the complement
  operation
• Blue axioms (especially 15) are different from
  regular algebra

5
Comments on the axioms

• The associative laws show that there is no
  ambiguity about a term such as x y z or xyz,
  so we can introduce multiple-input primitive
  gates
• The left and right columns of axioms are duals
• exchange all ANDs with ORs, and 0s with 1s
• The dual of any equation is always true

6
Are these axioms for real?

• We can show that these axioms are valid, given
  the definitions of AND, OR and NOT
• The first 11 axioms are easy to see from these
  truth tables alone. For example, x x 1
  because of the middle two lines below (where y
  x)

7
Proving the rest of the axioms

• We can make up truth tables to prove (both parts
  of) DeMorgans law
• For (x y) xy, we can make truth tables for
  (x y) and for xy
• In each table, the columns on the left (x and y)
  are the inputs. The columns on the right are
  outputs.
• In this case, we only care about the columns in
  blue. The other outputs are just to help us
  find the blue columns.
• Since both of the columns in blue are the same,
  this shows that (x y) and xy are equivalent

8
Simplification with axioms

• We can now start doing some simplifications

xy xyz xy x(y y) xyz
Distributive xy xy x(y y) x?1
xyz Axiom 7 y y 1 x xyz Axiom
2 x?1 x (x x)(x yz)
Distributive 1 ? (x yz) Axiom 7 x x
1 x yz Axiom 2
9
Lets compare the resulting circuits

• Here are two different but equivalent circuits.
• In general the one with fewer gates is better
• It costs less to build
• It requires less power
• But we had to do some work to find the second
  form

10
Some more laws

• Here are some more useful laws (p. 37). Notice
  the duals again!
• We can prove these laws by either
• Making truth tables
• Using the axioms

x xy (x x)(x y) Distributive 1 ?
(x y) x x 1 x y Axiom 2
11
The complement of a function

• The complement of a function always outputs 0
  where the original function outputted 1, and 1
  where the original produced 0.
• In a truth table, we can just exchange 0s and 1s
  in the output column(s)

f(x,y,z) x(yz yz)
12
Complementing a function algebraically

• You can use DeMorgans law to keep pushing the
  complements inwards
• You can also take the dual of the function, and
  then complement each literal
• If f(x,y,z) x(yz yz)
• the dual of f is x (y z)(y z)
• then complementing each literal gives x (y
  z)(y z)
• so f(x,y,z) x (y z)(y z)

f(x,y,z) x(yz yz) f(x,y,z) ( x(yz
yz) ) complement both sides x (yz
yz) because (xy) x y x (yz)
(yz) because (x y) x y x (y
z)(y z) because (xy) x y, twice
13
Standard forms of expressions

• We can write expressions in many ways, but some
  ways are more useful than others
• A sum of products (SOP) expression contains
• Only OR (sum) operations at the outermost level
• Each term that is summed must be a product of
  literals
• The advantage is that any sum of products
  expression can be implemented using a two-level
  circuit
• literals and their complements at the 0th level
• AND gates at the first level
• a single OR gate at the second level
• This diagram uses some shorthands
• NOT gates are implicit
• literals are reused
• this is not okay in LogicWorks!

f(x,y,z) y xyz xz
14
Minterms

• A minterm is a special product of literals, in
  which each input variable appears exactly once.
• A function with n variables has 2n minterms
  (since each variable can appear complemented or
  not)
• A three-variable function, such as f(x,y,z), has
  23 8 minterms
• Each minterm is true for exactly one combination
  of inputs

xyz xyz xyz xyz xyz xyz xyz xyz
Minterm Is true when Shorthand xyz x0, y0,
z0 m0 xyz x0, y0, z1 m1 xyz x0, y1,
z0 m2 xyz x0, y1, z1 m3 xyz x1, y0,
z0 m4 xyz x1, y0, z1 m5 xyz x1, y1,
z0 m6 xyz x1, y1, z1 m7
15
Sum of minterms form

• Every function can be written as a sum of
  minterms, which is a special kind of sum of
  products form
• The sum of minterms form for any function is
  unique
• If you have a truth table for a function, you can
  write a sum of minterms expression just by
  picking out the rows of the table where the
  function output is 1.

f xyz xyz xyz xyz xyz m0
m1 m2 m3 m6 ?m(0,1,2,3,6)
f xyz xyz xyz m4 m5 m7
?m(4,5,7)
f contains all the minterms not in f
16
The dual idea products of sums

• Just to keep you on your toes...
• A product of sums (POS) expression contains
• Only AND (product) operations at the outermost
  level
• Each term must be a sum of literals
• Product of sums expressions can be implemented
  with two-level circuits
• literals and their complements at the 0th level
• OR gates at the first level
• a single AND gate at the second level
• Compare this with sums of products

f(x,y,z) y (x y z) (x z)
17
Maxterms

• A maxterm is a sum of literals, in which each
  input variable appears exactly once.
• A function with n variables has 2n maxterms
• The maxterms for a three-variable function
  f(x,y,z)
• Each maxterm is false for exactly one combination
  of inputs

x y z x y z x y z x y z x
y z x y z x y z x y z
Maxterm Is false when Shorthand x y z x0,
y0, z0 M0 x y z x0, y0, z1 M1 x y
z x0, y1, z0 M2 x y z x0, y1,
z1 M3 x y z x1, y0, z0 M4 x y
z x1, y0, z1 M5 x y z x1, y1,
z0 M6 x y z x1, y1, z1 M7
18
Product of maxterms form

• Every function can be written as a unique product
  of maxterms
• If you have a truth table for a function, you can
  write a product of maxterms expression by picking
  out the rows of the table where the function
  output is 0. (Be careful if youre writing the
  actual literals!)

f (x y z)(x y z)(x y z) M4
M5 M7 ?M(4,5,7)
f (x y z)(x y z)(x y z) (x
y z)(x y z) M0 M1 M2 M3 M6
?M(0,1,2,3,6)
f contains all the maxterms not in f
19
Minterms and maxterms are related

• Any minterm mi is the complement of the
  corresponding maxterm Mi
• For example, m4 M4 because (xyz) x y
  z

Maxterm Shorthand x y z M0 x y z M1 x
y z M2 x y z M3 x y z M4 x
y z M5 x y z M6 x y z M7
Minterm Shorthand xyz m0 xyz m1 xyz m
2 xyz m3 xyz m4 xyz m5 xyz m6 xyz m
7
20
Converting between standard forms

• We can convert a sum of minterms to a product of
  maxterms
• In general, just replace the minterms with
  maxterms, using maxterm numbers that dont appear
  in the sum of minterms
• The same thing works for converting from a
  product of maxterms to a sum of minterms

From before f ?m(0,1,2,3,6) and f
?m(4,5,7) m4 m5 m7 complementing (f)
(m4 m5 m7) so f m4 m5 m7 DeMorgans
law M4 M5 M7 By the previous page
?M(4,5,7)
f ?m(0,1,2,3,6) ?M(4,5,7)
21
Summary so far

• So far
• A bunch of Boolean algebra trickery for
  simplifying expressions and circuits
• The algebra guarantees us that the simplified
  circuit is equivalent to the original one
• Introducing some standard forms and terminology
• Next
• An alternative simplification method
• Well start using all this stuff to build and
  analyze bigger, more useful, circuits

22
Karnaugh maps

• Last time we saw applications of Boolean logic to
  circuit design.
• The basic Boolean operations are AND, OR and NOT.
• These operations can be combined to form complex
  expressions, which can also be directly
  translated into a hardware circuit.
• Boolean algebra helps us simplify expressions and
  circuits.
• Today well look at a graphical technique for
  simplifying an expression into a minimal sum of
  products (MSP) form
• There are a minimal number of product terms in
  the expression.
• Each term has a minimal number of literals.
• Circuit-wise, this leads to a minimal two-level
  implementation.

23
Review Standard forms of expressions

• We can write expressions in many ways, but some
  ways are more useful than others
• A sum of products (SOP) expression contains
• Only OR (sum) operations at the outermost level
• Each term that is summed must be a product of
  literals
• The advantage is that any sum of products
  expression can be implemented using a two-level
  circuit
• literals and their complements at the 0th level
• AND gates at the first level
• a single OR gate at the second level
• This diagram uses some shorthands
• NOT gates are implicit
• literals are reused
• this is not okay in LogicWorks!

f(x,y,z) y xyz xz
24
Terminology Minterms

• A minterm is a special product of literals, in
  which each input variable appears exactly once.
• A function with n variables has 2n minterms
  (since each variable can appear complemented or
  not)
• A three-variable function, such as f(x,y,z), has
  23 8 minterms
• Each minterm is true for exactly one combination
  of inputs

xyz xyz xyz xyz xyz xyz xyz xyz
Minterm Is true when Shorthand xyz x0, y0,
z0 m0 xyz x0, y0, z1 m1 xyz x0, y1,
z0 m2 xyz x0, y1, z1 m3 xyz x1, y0,
z0 m4 xyz x1, y0, z1 m5 xyz x1, y1,
z0 m6 xyz x1, y1, z1 m7
25
Terminology Sum of minterms form

• Every function can be written as a sum of
  minterms, which is a special kind of sum of
  products form
• The sum of minterms form for any function is
  unique
• If you have a truth table for a function, you can
  write a sum of minterms expression just by
  picking out the rows of the table where the
  function output is 1.

f xyz xyz xyz xyz xyz m0
m1 m2 m3 m6 ?m(0,1,2,3,6)
f xyz xyz xyz m4 m5 m7
?m(4,5,7)
f contains all the minterms not in f
26
Re-arranging the truth table

• A two-variable function has four possible
  minterms. We can re-arrange these minterms into a
  Karnaugh map.
• Now we can easily see which minterms contain
  common literals.
• Minterms on the left and right sides contain y
  and y respectively.
• Minterms in the top and bottom rows contain x
  and x respectively.

27
Karnaugh map simplifications

• Imagine a two-variable sum of minterms
• xy xy
• Both of these minterms appear in the top row of a
  Karnaugh map, which means that they both contain
  the literal x.
• What happens if you simplify this expression
  using Boolean algebra?

xy xy x(y y) Distributive x ?
1 y y 1 x x ? 1 x
28
More two-variable examples

• Another example expression is xy xy.
• Both minterms appear in the right side, where y
  is uncomplemented.
• Thus, we can reduce xy xy to just y.
• How about xy xy xy?
• We have xy xy in the top row, corresponding
  to x.
• Theres also xy xy in the right side,
  corresponding to y.
• This whole expression can be reduced to x y.

29
A three-variable Karnaugh map

• For a three-variable expression with inputs x, y,
  z, the arrangement of minterms is more tricky
• Another way to label the K-map (use whichever you
  like)

30
Why the funny ordering?

• With this ordering, any group of 2, 4 or 8
  adjacent squares on the map contains common
  literals that can be factored out.
• Adjacency includes wrapping around the left and
  right sides
• Well use this property of adjacent squares to do
  our simplifications.

xyz xyz xz(y y) xz ? 1 xz
xyz xyz xyz xyz z(xy xy
xy xy) z(y(x x) y(x
x)) z(yy) z
31
Example K-map simplification

• Lets consider simplifying f(x,y,z) xy yz
  xz.
• First, you should convert the expression into a
  sum of minterms form, if its not already.
• The easiest way to do this is to make a truth
  table for the function, and then read off the
  minterms.
• You can either write out the literals or use the
  minterm shorthand.
• Here is the truth table and sum of minterms for
  our example

32
Unsimplifying expressions

• You can also convert the expression to a sum of
  minterms with Boolean algebra.
• Apply the distributive law in reverse to add in
  missing variables.
• Very few people actually do this, but its
  occasionally useful.
• In both cases, were actually unsimplifying our
  example expression.
• The resulting expression is larger than the
  original one!
• But having all the individual minterms makes it
  easy to combine them together with the K-map.

xy yz xz (xy ? 1) (yz ? 1) (xz ?
1) (xy ? (z z)) (yz ? (x x)) (xz ?
(y y)) (xyz xyz) (xyz xyz)
(xyz xyz) xyz xyz xyz xyz
33
Making the example K-map

• Next up is drawing and filling in the K-map.
• Put 1s in the map for each minterm, and 0s in the
  other squares.
• You can use either the minterm products or the
  shorthand to show you where the 1s and 0s belong.
• In our example, we can write f(x,y,z) in two
  equivalent ways.
• In either case, the resulting K-map is shown
  below.

34
K-maps from truth tables

• You can also fill in the K-map directly from a
  truth table.
• The output in row i of the table goes into square
  mi of the K-map.
• Remember that the rightmost columns of the K-map
  are switched.

35
Grouping the minterms together

• The most difficult step is grouping together all
  the 1s in the K-map.
• Make rectangles around groups of one, two, four
  or eight 1s.
• All of the 1s in the map should be included in at
  least one rectangle.
• Do not include any of the 0s.
• Each group corresponds to one product term. For
  the simplest result
• Make as few rectangles as possible, to minimize
  the number of products in the final expression.
• Make each rectangle as large as possible, to
  minimize the number of literals in each term.
• Its all right for rectangles to overlap, if that
  makes them larger.

36
Reading the MSP from the K-map

• Finally, you can find the MSP.
• Each rectangle corresponds to one product term.
• The product is determined by finding the common
  literals in that rectangle.
• For our example, we find that xy yz xz yz
  xy. (This is one of the additional algebraic
  laws from last time.)

37
Practice K-map 1

• Simplify the sum of minterms m1 m3 m5 m6.

38
Solutions for practice K-map 1

• Here is the filled in K-map, with all groups
  shown.
• The magenta and green groups overlap, which makes
  each of them as large as possible.
• Minterm m6 is in a group all by its lonesome.
• The final MSP here is xz yz xyz.

39
Four-variable K-maps

• We can do four-variable expressions too!
• The minterms in the third and fourth columns, and
  in the third and fourth rows, are switched
  around.
• Again, this ensures that adjacent squares have
  common literals.
• Grouping minterms is similar to the
  three-variable case, but
• You can have rectangular groups of 1, 2, 4, 8 or
  16 minterms.
• You can wrap around all four sides.

40
Example Simplify m0m2m5m8m10m13

• The expression is already a sum of minterms, so
  heres the K-map
• We can make the following groups, resulting in
  the MSP xz xyz.

41
K-maps can be tricky!

• There may not necessarily be a unique MSP. The
  K-map below yields two valid and equivalent MSPs,
  because there are two possible ways to include
  minterm m7.
• Remember that overlapping groups is possible, as
  shown above.